December 2, 2016
Published by Stephan Sponar
Uncertainty Relations
Heisenberg’s uncertainty principle is without any doubt one of the cornerstones of modern quantum physics. However, several formulations coexist which address different physical scenarios. Heisenberg’s uncertainty principle in a formulation of standard deviations, i.e., uncertainties intrinsic to any quantum system, is uncontroversial and demonstrated in various quantum systems. Probably it’s most well-known formulation, as the product of the position and momentum standard deviations given by . However, uncertainty relations in terms of standard deviations describe the limitation of preparing quantum objects and have no direct relevance to the limitation of measurements on single systems, as originally suggested by Heisenberg. His starting point is a relation between the precision (mean error) of a position measurement and the disturbance it induces on a subsequent momentum measurement of a particle – more precisely of an electron. This is beautifully captured in the famous γ-ray microscope thought experiment, which is solely based on the Compton-effect.
July 1, 2021
Published by Stephan Sponar
According to the uncertainty principle, which is a corner stone of quantum mechanics, it is impossible to measure both position and momentum of an elementary particle (e.g. electron as in Heisenberg’s original argument) with arbitrary accuracy or in other word with zero error. One of the major problems in quantum physics has been to generalize the classical root-mean-square error to quantum measurements to obtain an error measure satisfying both soundness (to vanish for any accurate measurements) and completeness (to vanish only for accurate measurements).
June 6, 2021
Published by Stephan Sponar
We experimentally tested a tight information-theoretic measurement uncertainty relation, in terms of a proposed three-outcome POVM using neutron spin-1/2 qubits. The obtained results of the noise-disturbance trade-off relation for three-outcome POVM outperform prior results for projective measurements. The obtained results violate the lower bound for projective measurements as theoretically predicted.
September 30, 2020
Published by Stephan Sponar
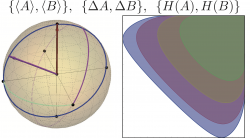
In our neutron polarimetric experiment we study tight state-independent preparation uncertainty relations for quits. The tight relations are based on the relationship between the expectation values of Pauli spin observables and two standard measures of uncertainty, namely standard deviations and Shannon entropies . We present a neutron polarimetric test of the tight state-independent preparation uncertainty relations for orthogonal, as well as non-orthogonal, Pauli spin observables. The final results, obtained with pure and mixed spin states, reproduce the theoretical predictions evidently for arbitrary initial states of variable degree of polarization.
January 15, 2018
Published by Stephan Sponar
In our neutron optical experiment we test a tight information-theoretic uncertainty relation with neutron spin-1/2 qubits. The noise associated to the measurement of an observable is defined via conditional Shannon entropies and a trade-off relation between the noises for two arbitrary spin observables is demonstrated. This is achieved by implementing four-outcome positive-operator valued measure POVMs. The optimal bound of this tradeoff is experimentally obtained for various non-commuting spin observables. For some of these observables this lower bound can be reached with projective measurements, but we observe that, in other cases, the tradeoff is only saturated by general quantum measurements (i.e., positive-operator valued measures), as predicted theoretically.
September 4, 2017
Published by Stephan Sponar
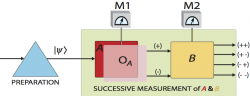
Since the theoretical findings of Masanao Ozawa, namely a violating and thus a necessary reformulation of Heisenberg’s original error-disturbance uncertainty relation, this particular field has experienced increased attention. However, soon after publication of our experimental verification an alternative theory was presented by Paul Busch, and Pekka Lahti, and Reinhard F. Werner (BLW) which in contrast stated the validity of Heisenberg’s relation. We now carried out the first experimental comparison of these two competing approaches leading to a surprising result: Despite the strong controversy, in case of projectively measured qubit observables both approaches even lead to equal outcomes.
December 16, 2016
Published by Stephan Sponar
The indeterminacy inherent in quantum measurements is an outstanding character of quantum theory, which manifests itself typically in the uncertainty principle. In the last decade, several universally valid forms of error-disturbance uncertainty relations were derived for completely general quantum measurements for arbitrary states. An optimal form for spin measurements for some pure states was established recently. However, the bound in his inequality is not stringent for mixed states. Masanao Ozawa derived a new bound tight in the corresponding mixed state case, which was tested by our group. We experimentally observed the attainability of the new bound.
December 15, 2016
Published by Stephan Sponar
Information is a key quantity in science and plays a significant role in many economic sectors such as communication technologies, cryptography, or data storage. In quantum communication and information technology the transfer and encryption of information is studied; in the quantum regime phenomena such as the Heisenberg uncertainty principle have to be taken into account as well. By using the so-called information entropy, we precisely analyze uncertainty in terms of “knowledge” and “predictability” and established a trade-off relation between them. These concepts play a central role in the theory of communication, engineering and computer science.
September 2, 2016
Published by Stephan Sponar
Heisenberg’s uncertainty principle. is certainly one of the most famous foundations of quantum physics. According to this principle, not all properties of a quantum particle are determined with arbitrary accuracy. In the early days of quantum theory, this has often been justified by the notion that every measurement inevitably recoils the quantum particle, which disturbs the results of any further measurements. This, however, turns out to be an oversimplification. In our neutron polarimetric experiment different sources of quantum uncertainty could now be distinguished, validating theoretical results of an error-disturbance uncertainty relation proposed by Masanao Ozawa and a new tight inequality.