 May 19, 2017
Published by Stephan Sponar
May 19, 2017
Published by Stephan Sponar
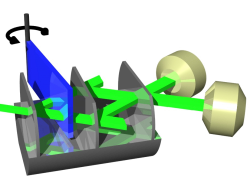
Neutron interferometry is based on the wave nature of neutrons. Inside the interferometer partial wave-function of the sub-beams in the individual interferometer paths are created and recombined coherently afterwards, resulting in interference effects. The first fully operating neutron interferometer was produced and demonstrated successfully in 1974 by Prof. Rauch at the Atominstitut Vienna, Austria – a sensational find.
 October 2, 2016
Published by Stephan Sponar
October 2, 2016
Published by Stephan Sponar
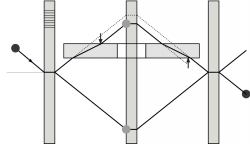
Thermal neutrons passing a slab of material undergo a phase shift and a spatial displacement. Both effects are coupled in most situations. However, using an appropriate configuration of phase shifters they can be decoupled. In addition topics such as dual phase shifters as well as phase shifts of perfect crystal samples are discussed.
 October 11, 2015
Published by Stephan Sponar
October 11, 2015
Published by Stephan Sponar
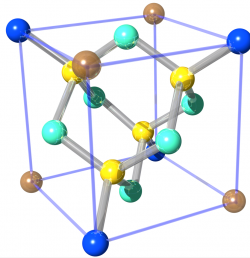
Generally speaking a single crystal or monocrystalline solid is a material in which the crystal lattice of the entire sample is continuous and unbroken to the edges of the sample. In the case of silicon the lattice is of diamond type, a variation of face centered cubic crystal structure. The diamond lattice can be viewed as a pair of intersecting face-centered cubic lattices, with each separated by 1/4 of the width of the unit cell.
 May 18, 2015
Published by Stephan Sponar
May 18, 2015
Published by Stephan Sponar
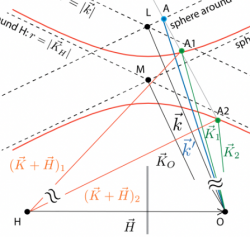
Compared to the geometrical theory, the dynamical theory of diffraction takes the spatial periodicity of the interaction potential in perfect single crystals into account. Thereby the Schrödinger equation has to be solved within this potential. When neutrons illuminate a perfect crystal under near-Bragg orientation conditions, the dynamical theory of diffraction predicts a coherent splitting of the incident wave into four components, with two traveling wave components passing within the crystal in the Bragg direction and two components in the forward (incident) direction.
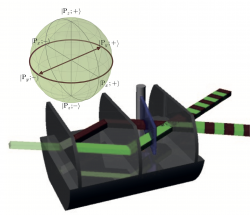 July 11, 2014
Published by Stephan Sponar
July 11, 2014
Published by Stephan Sponar
The interferometer can be formally treated as a two-level system (qubit) – more precisely as a “pseudospin“. The two eigenstates of the two-level system are formed by the paths inside the interferometer generally referred to as path I or “1” and path II or “0”.




