October 25, 2016
Published by Stephan Sponar
Quantum Contextuality
Contextuaily occupies a peculiar position in quantum theory, it is an even more fundament property than entanglement. Entanglement occurs in quantum systems that consist of space-like separated parts or—more generally—in systems whose observables belong to disjoint Hilbert spaces. The latter is the case for instance for spin, path and energy degree of freedom in the single-neutron systems, where entanglement and Contextuaily may coexist – but contextually does nor require entanglement in general. Apart from Bell’s theorem, there exists a second powerful argument against the possibility of extending QM into a more complete theory, namely the Kochen–Specker (KS) theorem. The KS theorem sets certain constraints on classes of hidden variable theories, more precisely non-contextual hidden variable theories, which try to explain the apparent randomness of quantum mechanics as a deterministic model featuring hidden states.
July 3, 2024
Published by Stephan Sponar
The question whether measurable quantities of a quantum object have definite values prior to the actual measurement is a fundamental issue ever since quantum theory has been introduced in the early 20th century. Leggett-Garg inequalities (LGIs) study temporal correlations of a single system, which are derived under the assumption of so called macro-realism. There it is assumed, that any (macroscopic) object, which may occur in two (or more) macroscopically distinct states, is at any given time in a definite one of those states. The predictions of quantum mechanics stand in stark contradiction with these realistic theories, which manifest in violations of LGIs.
November 9, 2017
Published by Stephan Sponar
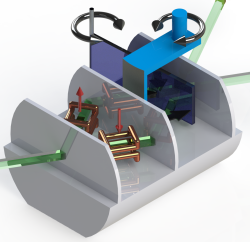
Up to date alle experimental tests of quantum contextuality based on the Bell-Kochen-Specker (BKS) theorem have demonstrated that not all observables among a given set can be assigned non-contextual eigenvalue predictions, but have never identified which specific observables must fail to do so. We have now overcome this hurdle by demonstrating that BKS contextuality can be confined to particular observables by pre- and postselection, resulting in anomalous weak values obtained in neutron interferometry.
September 20, 2017
Published by Stephan Sponar
The Kochen-Specker (KS) Theorem sets constrains on hidden-variable theories which try to explain the randomness of quantum mechanics in terms of a as a deterministic theory. We perform experimental tests of the Kochen-Specker theorem based on an inequality derived from the Peres-Mermin proof, using spin-path (momentum) entanglement in a single neutron system. In our recent experiment we demonstrate localized quantum contextuality in a neutron interferometric experiment.
September 22, 2016
Published by Stephan Sponar
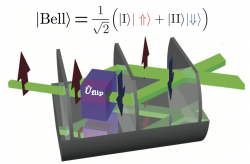
The remarkable discovery made by John S. Bell, namely that quantum mechanics cannot be counterfactual (definiteness of results prior to measurement) and local (physical objects are only influenced by its immediate surroundings) gave rise to a number of experiments probing the foundations quantum mechanics. We prepare our neutrons in a spin-path entangled state and measure correlations that arise between observables of otherwise independent degrees of freedom in the single neutron system in order to validate the presence of entanglement.
September 21, 2016
Published by Stephan Sponar
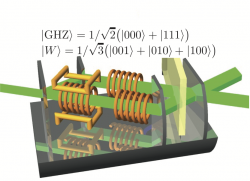
Greenberger–Horne–Zeilinger (GHZ) and W states represent two very different kinds of tripartite entanglement. We prepare entanglement between the spin, path, and (total) energy degrees of freedom, in a single-neutron system. We implemented a triply entangled GHZ–like states, as well as W states, and coherently manipulated relative phases of two-level quantum subsystems.
November 29, 2014
Published by Stephan Sponar
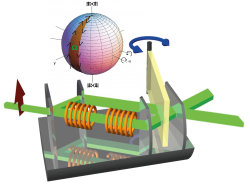
The influence of the geometric phase on a Bell measurement expressed in terms of the Clauser-Horne-Shimony-Holt (CHSH) inequality, is observed for a spin-path-entangled neutron state in an interferometric setup. It is experimentally demonstrated that the effect of geometric phase can be balanced by a change in Bell angles. The geometric phase is acquired during a time-dependent interaction with a radiofrequency field. Two schemes, polar and azimuthal adjustment of the Bell angles, are realized and analyzed in detail.