Experimental test of entropic noise-disturbance uncertainty relations for three-outcome qubit measurements
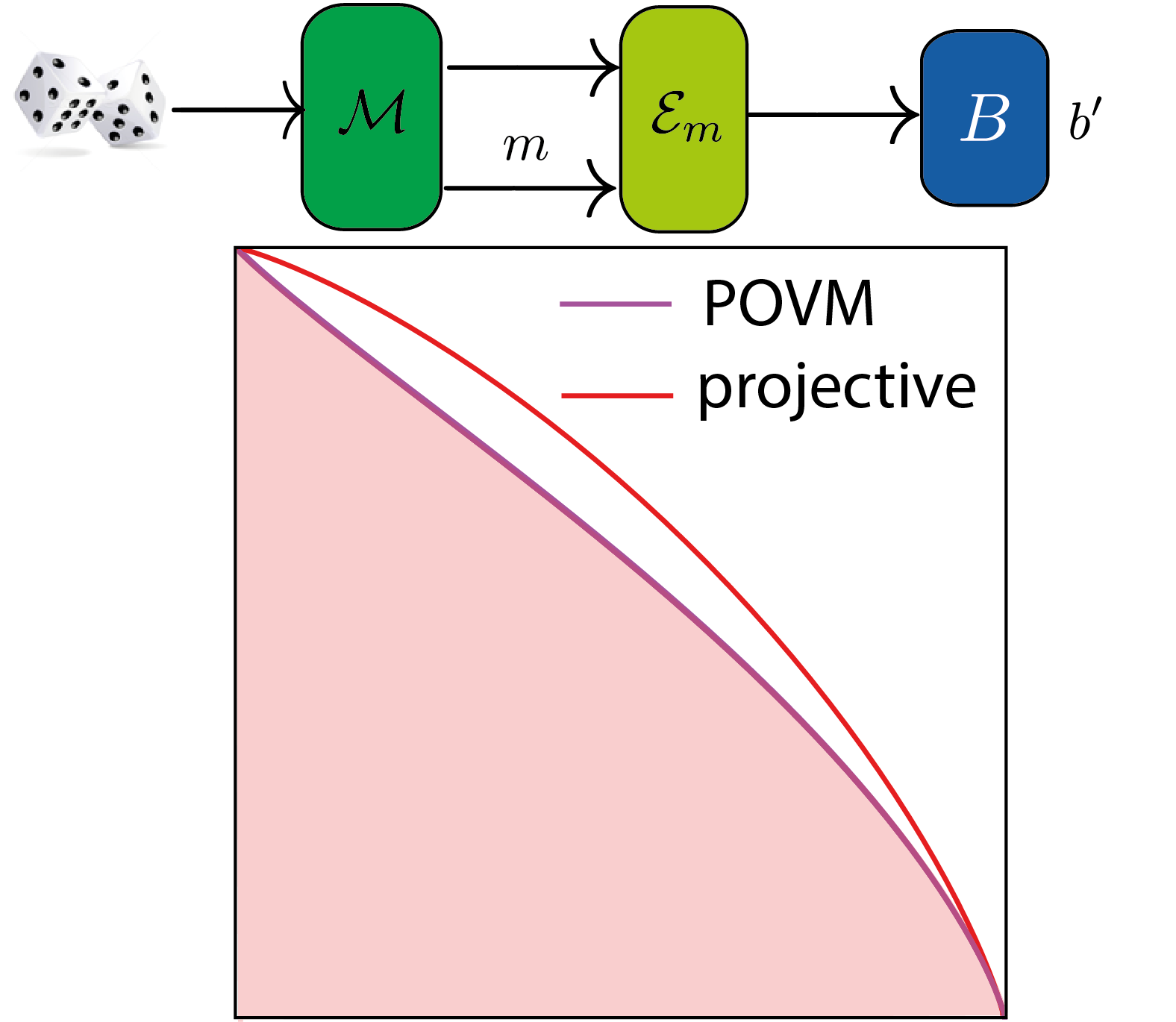
June 6, 2021 11:27 amIn our latest work 1, we experimentally tested a tight information-theoretic measurement uncertainty relation, in terms of a proposed three-outcome POVM using neutron spin-1/2 qubits. Previously (see here for details) we reported a tight noise-disturbance uncertainty relation for projective qubit measurements 2. Meanwhile, new theoretical analysis 3 predicts that projective measurements suboptimal, with respect to the noise-disturbance trade-offs, compared to generalized (or unsharp) measurements (see here for theoretical details). We developed a new experimental technique to realize general measurements, more precisely a three-outcome positive-operator valued measure (POVM), allowing to test the suboptimal nature of projective measurements regarding noise – disturbance uncertainty realtions. In the present manuscript we provide experimental evidence that when performing such general measurements, on a qubit system (in our case a neutron spin), tighter bounds of the noise-disturbance trade-offs are observed compared to projective measurements. This advantage of POVMs over projective measurements on noise-disturbance uncertainty relations has not previously been observed experimentally.
While several definitions of noise have previously been studied theoretically and experimentally, we utilize the information-theoretic approach formulated as follows. Let be the eigenstates of the d-dimensional target observable A and measurement device being a collection of completely positive (CP) trace-nonincreasing maps . The instrument uniquely defines a positive-operator valued measure (POVM), denoted as . The noise is defined in the following scenario: the eigenstates of A are randomly prepared with probability before is applied, producing an outcome m with probability . If accurately measures A then the value of m should allow one to infer a; if the measurement is noisy, m yields less information about a. This noise is quantified in terms of the conditional Shannon entropy: denoting the random variables associated with a and m as and , respectively, the noise of for a measurement of A is , where and can be calculated from Bayes’ theorem. A schematical illautration of the noise scenario is deoicted below in panel (a).
The entropic disturbance of the apparatus on the measurement of B is defined with respect to an analogous procedure as the noise. Uniformly distributed eigenstates with eigenvalues associated with random variable are fed to the same instrument from which a post-measurement state emerges. In the disturbance configuration there is an additional subsequent measurement of observable B with outcomes . Due to the disturbing nature of the measurement apparatus , generally, a loss of correlation occurs. A subtle, yet important addendum to the concept of disturbance are error corrections. After measurement by , the state decomposed to the eigenstates of the measurement observables can be further transformed by a quantum operation dependent on the pointer value m of the apparatus. The disturbance is defined as the conditional entropy as , which is illustrated below in panel (b).

Using these notions of noise and disturbance, for arbitrary observables A and B in finite-dimensional Hilbert spaces, the noise-disturbance (measurement) relation holds. In 2 we experimentally tested , where is the inverse of the function defined as , with , for maximally incompatible qubit observables A and B. As it turned out, the proof given in 2 for this relation was incorrect and this relation does not hold in general, which was pointed out in 3. It should be noted that the relation does hold for projective measurements , although it can be violated by non-projective measurements. This bound can be violated by considering a three-outcome measurement , proposed in ba Branciard in 3, with the associated positive-operator valued measure (POVM) given by for , where
Noise-measurement: Uniformly distributed eigenstates of the observable , denoted as , are sent onto the apparatus , which is illustrated below in panel (c). The correlation between the eigenvalue corresponding to the state prepared and the outcome measured by the apparatus is used to determine the noise . This correlation is quantitatively characterized by the joint probability distribution . The conditional probability is then obtained via , allowing to calculate the noise using . The noise of the three-outcome POVM is determined applying the reduced setup, where the detector 1 (He cylindric count tube, diameter one inch) is directly mounted onto the exit window of the second supermirror to maintain optimal positioning when the supermirror is rotated (to implement the POVM weights), as illustrated and depicted below.


With this configuration a maximal count rate cnts/sec is recorded. During the measurement the POVM parameter is varied between and 0 in steps of . For each value of three intensities, belonging to the POVM outputs , , and (denoted as with ) are recorded in a measurement time 400 sec., which is plotted below For each value of an initial state (eigenstate of ) is chosen by random generator. The result is blinded during the measurement but stored in a data file for a later comparison with the obtained values for the noise .

Normalized and background corrected data of and , accounting for the joint probability . Using the theoretical prediction of the sum of the two probabilities given by , the joint probabilities and can be derived for each individual value of as seen below very left plots.

Using the conditional probabilities and are calculated, which is depicted together with the theoretical predictions in above right side. The theoretical predictions (red and blue curves) for the conditional probabilities are given by . With the six conditional probabilities we can calculate the noise via , with . The final results of the noise measurement , together with the theoretic prediction for the three-outcome POVM measurement and , for projective measurements, can be seen below (blue and green curve respectively).

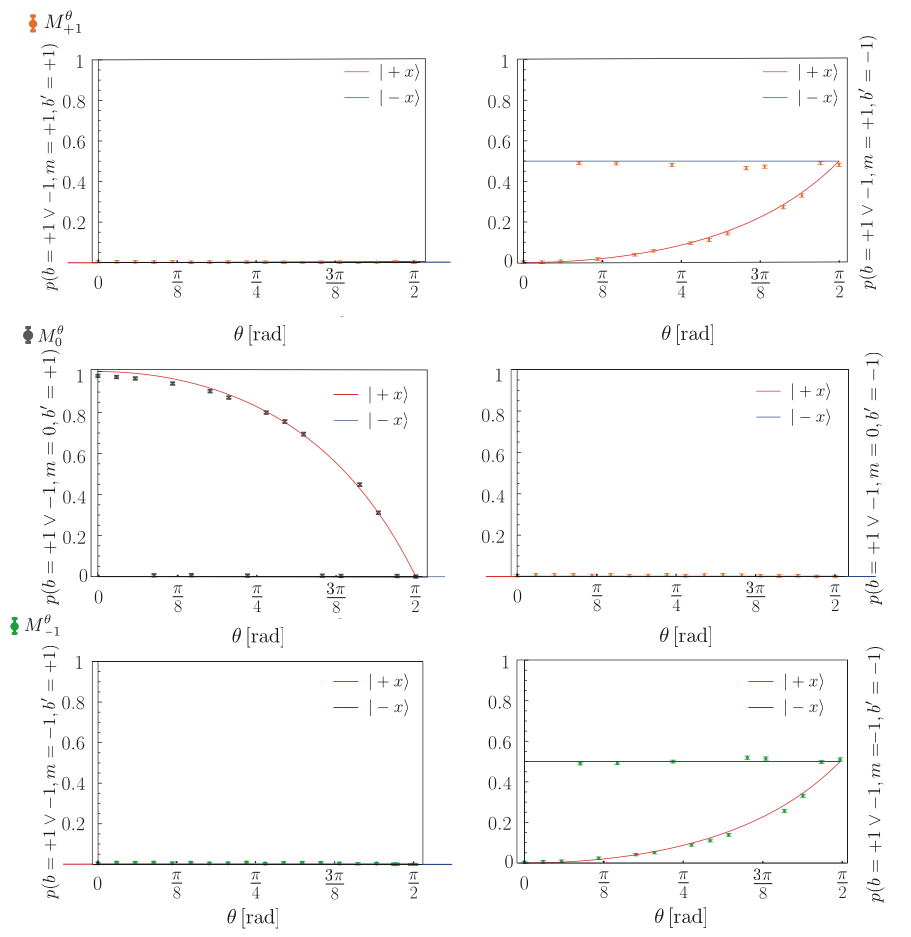
Disturbance-measurement: For the disturbance measurement the three-outcome POVM measurement is followed by a subsequent projective measurement of an observable . In addition, an optimal correction operation in between the two measurements maps and onto the negative x-axis and onto the positive x-axis, respectively, as schematically illustrated and pictured below.


Uniformly distributed eigenstates of the observable B, denoted as which are associated with random variable , are fed to the same instrument . Due to the disturbing nature of the measurement apparatus , in general, a loss of correlation occurs. The correlation between the eigenvalue b corresponding to the state prepared and the outcome b’ of the second now projective measured, which will be used to define the disturbance, is characterized by the joint probability distribution , allowing to calculate the disturbance . In the actual experiment, the detector (Boron trifluoride cylindric count tube, diameter of 3 inch, and an active volume of length 30 cm) was placed transversal to the beam. This was done to account for the beam displacement caused by the tilt of the second supermirror, when setting the POVM weights. With this configuration a maximal count rate cnts/sec is recorded. During the measurement the POVM parameter is varied between and 0 in steps of . For each value of now six intensities , belonging to the +b and -b measurement of the POVM outputs , , and , are recorded in a measurement time of 400 seconds, which is plotted below (left). For each value of an initial state (being an eigenstate of ) is chosen by a random generator. Again, the result is blinded during the measurement but stored in a data file for a later comparison with the obtained values for the disturbance . The randomly generated sequence is also listed below (right).

Following the same procedure as for the noise, the count rates are normalized (and background corrected) by the total number of counts which gives the six probabilities with and , respectively and calculated as , which is plotted below.
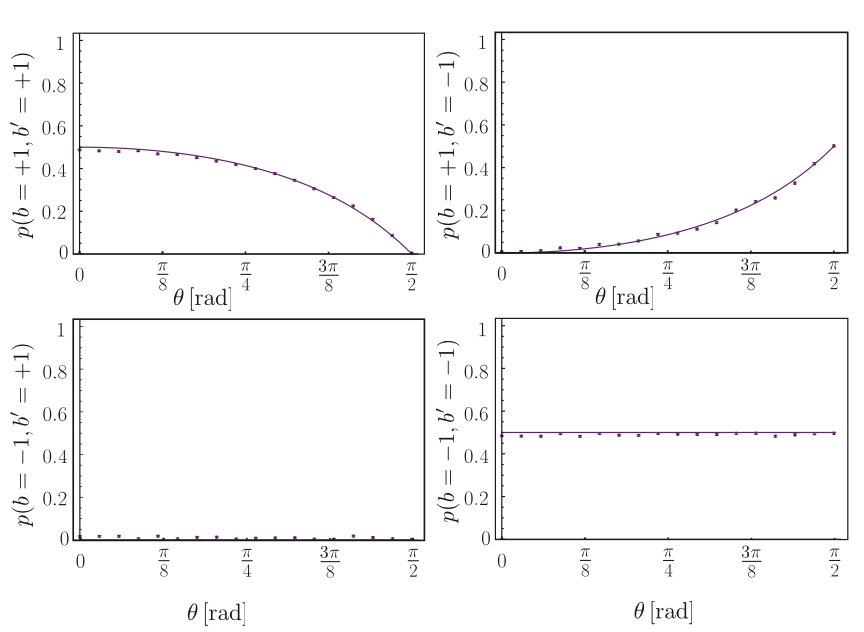
Again the data points are separated according to the input state and , which gives in total 12 probabilities with , and . Since the disturbance is defined as we need to calculate the joint probability via which can be seen below, with theoretical curves are given , plotted as purple lines.
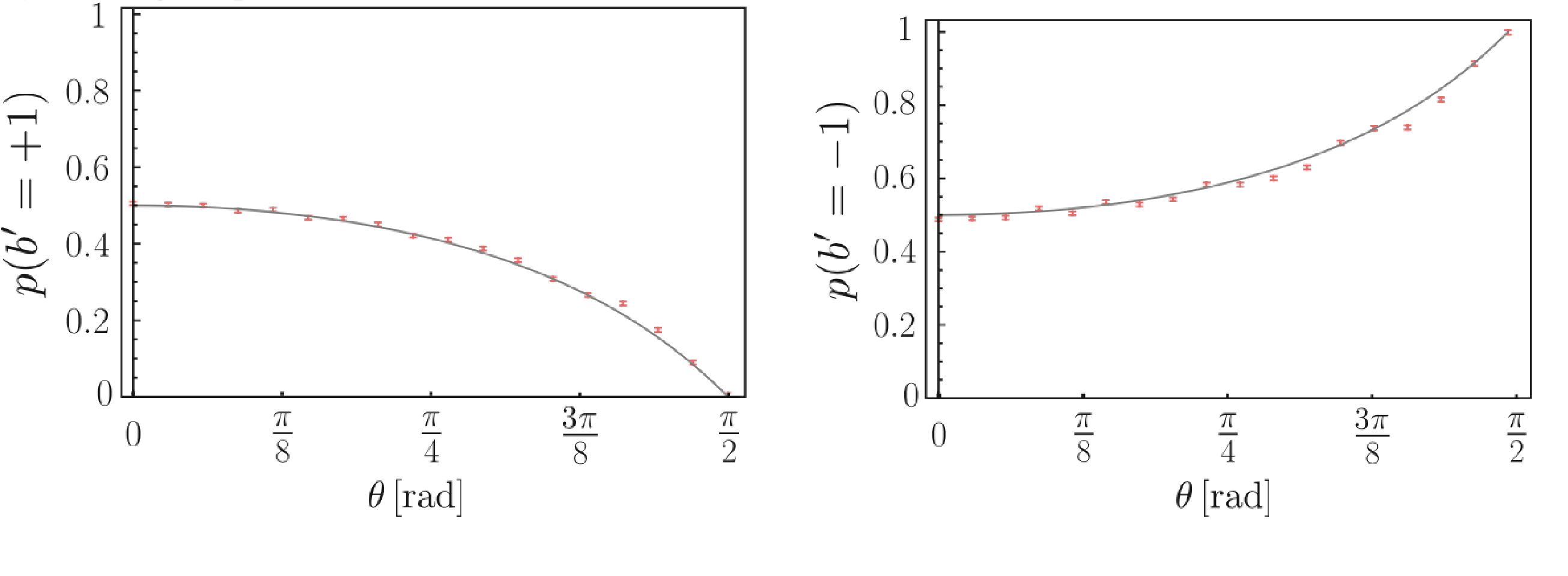
Now we calculate the marginal probabilities by summation of the data from above , with theoretical curves are given by , plotted as gray lines.
The obtained results of the POVM noise – disturbance trade off relations outperform prior results for projective measurements, over almost the entire measured range of the tested POVM parameter θ below (left), which becomes apparent in the noise-disturbance plot below (right).
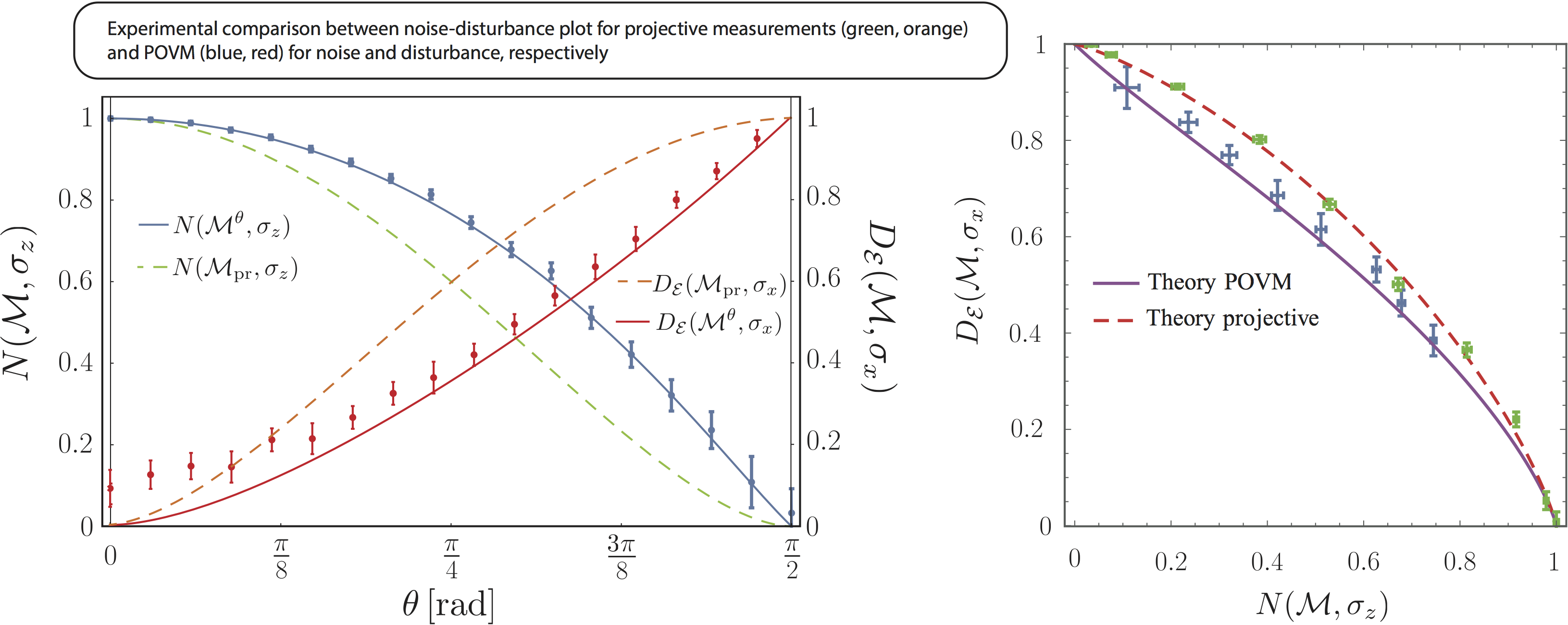
Finally, we want to emphasize that the plot above (left) gives an intuitive explanation why the three-outcome POVM outperforms projective measurements: although there is a loss coming from the noise in the POVM (meaning higher noise values compared to the projective measurement), this loss is surpassed by the gain in the obtained disturbance (significantly lower disturbance values as for projective measurement). This behavior is a peculiarity of the applied three-outcome POVM. In general, increasing the number of possible outcomes has a negative (increasing) effect on the noise-disturbance bound.
1. S. Sponar, A. Danner, V. Pecile, N. Einsidler, B. Demirel, and Y. Hasegawa Phys. Rev. Research 3, 023175 (2021). ↩
2. G. Sulyok, S. Sponar, B. Demirel, F. Buscemi, M. J. W. Hall, M. Ozawa, and Y. Hasegawa Phys. Rev. A 115, 030401 (2016). ↩
3. A. A. Abbott and C. Branciard, Phys. Rev. A 94, 062110 (2016). ↩