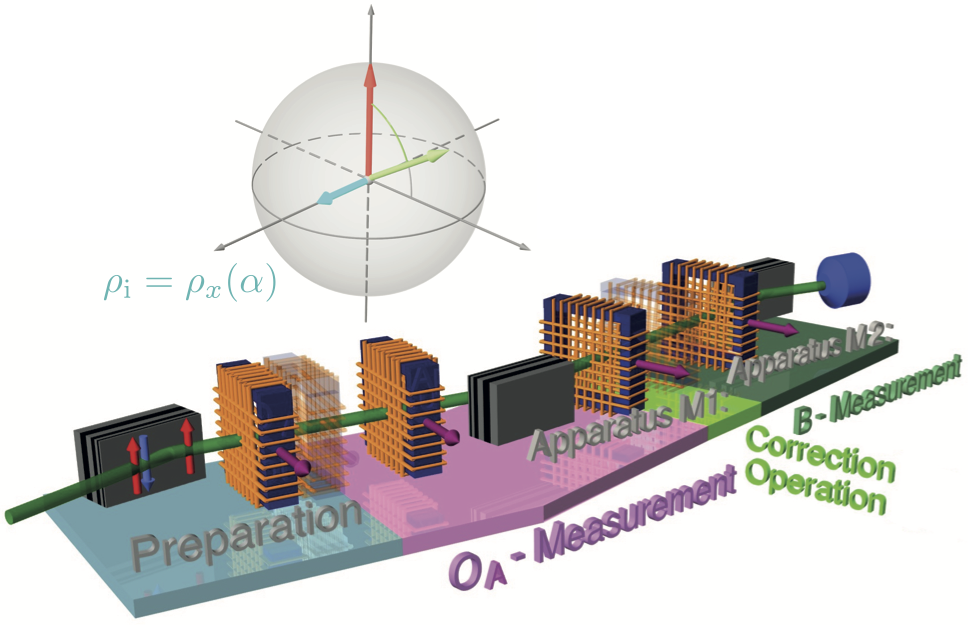
Mixed State Uncertainty Relations

The indeterminacy inherent in quantum measurements is an outstanding character of quantum theory, which manifests itself typically in the uncertainty principle. In the last decade, several universally valid forms of error-disturbance uncertainty relations were derived for completely general quantum measurements for arbitrary states.  An optimal form for spin measurements for some pure states was established recently. However, the bound in his inequality is not stringent for mixed states. Masanao Ozawa derived a new bound tight in the corresponding mixed state case, which was tested by out group and the results are presented  in the journal “Physical Review Letters”  ¹.

Aiming in of an improvement of error-disturbance uncertainty relations (EDUR) a stronger inequality was proposed  (see here for details of tight uncertainty relations). Later, it was pointed out that the relation above is not stringent for mixed states in general, when the Robertson bound is simply extended to , which decreases for mixed states and vanishes for totally mixed states. Further improvement of the bound was put forward by Masanao Ozawa who could show that the constant can be replaced by a stronger constant defined by . This new parameter coincides with the Robertson bound when is a pure state, but makes the EDUR stronger for a mixed ensemble.

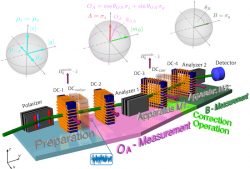
The experimental setup is depicted above. It consists of three stages: (i) Preparation (blue region): a monochromatic neutron beam is polarized in -direction by passing through a supermirror spin polarizer. In the coil (DC-1) the required directions of the input states are generated and the mixture is controlled via a tunable noisy magnetic field. (ii) Apparatus M1, consisting of a projective – measurement (pink region) and a correction operation (light green region): the first measurement is carried out by the analyzer-1 together with the coils (DC-3/4) followed by a unitary rotation of the output state of the – measurement. (iii) Apparatus M2, measuring   (dark green region): the second measurement is fixed to make a   – measurement, which is carried out by the the coil (DC-4) and the analyzer-2. Transparent coils are virtual and their positions are taken up by other DC-coils in practice. Note that transparent coils are virtual, in practice other dc coils fulfill their tasks. The mixing of the state can be tuned by applying a noise magnetic field . In practice we realize -rotations with noisy fields by one DC-coil (DC-1), where the required mixture can be adjusted by the amplitude of the noise signal. In the correction stage, the output sate of the – measurement is transformed by a unitary operator . One can realize the optimal correction by adjusting   as described in one of our previous experiments for pure states (see here for details).

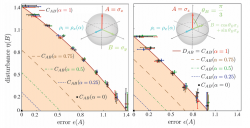
The influence of the mixture of the input states is studied, by applying the optimal correction procedure while tuning the input states . The results are plotted above (left). Each plot exhibits optimal EDUR for a particular mixture with theoretical predictions by and . It is immediately seen that the error-disturbance uncertainty is insensitive to dephasing or amplitude damping of the input states caused by the fluctuating magnetic field and that the bound is preserved perfectly. The measured values always saturate our inequality, for mixed spin states no dependence on mixture appears. Only the bound given by leads to saturation of the error-disturbance uncertainty relation. This statement is also true for different choices of the observables , which is plotted on the right side (details of the data treatment can be found here).

To summarize,  our experiment successfully demonstrates the tightness of the bound and the non-tightness of the simply extended Robertson bound  . We also confirmed the independence of the EDUR on the mixture of the states for observables   and  , with .

1. B. Demirel, S. Sponar, G. Sulyok, M. Ozawa, and Y. Hasegawa, Physical Review Letters 117, 140402 (2016)
[quant-ph/1511.03462]. ↩