Neutrons Optical Devices

Optics deals with waves and their transformation by objects, i.e., scattering. Accordingly, since quantum mechanics describes massive particles as traveling waves, neutron optics deals with scattering of the neutrons’ de Broglie (or matter) wave. The source of this phenomenon may be of solid nature – more precisely the fermi pseudo potential of atoms, or represented by magnetic fields which effect the neutron’s wave function likewise.

Contents:

Direct Current (DC) Spin Rotators

rrrrrrrrrrrrrrrrrrNext generation (3D-printed) Spin Rotators

Radio Frequency (RF) Spin Flippers

Supermirror Polarizer

Neutrons in magnetic fields: Larmor precession

The motion of a free propagating neutron, interacting with magnetic  is described by a nonrelativistic Schrödinger equation also referred to as Pauli equation, given by , where and are the mass (kg) and the magnetic moment (, with J/T) of the neutron, respectively and and contains the Pauli matrices . A solution is found by the two dimensional spinor wave function of the neutron, which is denoted as , with spatial wave function . The state vector for the spin eigenstates denoted as and is given by , introducing polar angle and azimuthal angle , which can be represented on a Bloch sphere as shown below (left). In the field of general two-level systems (qubits) the term Bloch sphere is conventionally used, whereas the term Poincaré sphere is more common for representation of light polarization.

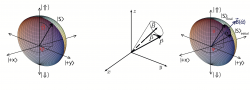
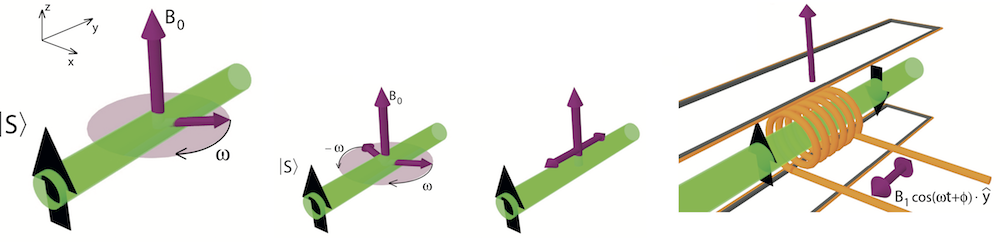
The neutron couples via its permanent magnetic dipole moment to magnetic fields, which is described by the Hamiltonian , where magnetic fields of stationary and/or time dependent origin are utilized for arbitrary spinor rotations in neutron optics. When a neutron enters a stationary magnetic field region (non-adiabatically), the motion of its polarization vector, defined as the expectation value of the Pauli spin matrices is described by the Bloch-equation, exhibiting Larmor precession: , where is a gyromagnetic ratio given by . This is the equation of motion of a classical magnetic dipole in a magnetic field, which shows the precession of the polarization vector about the magnetic field with the Larmor frequency , which is depicted above (right). The Larmor precession angle (rotation angle), solely depends on the strength of the applied magnetic field and the propagation within the field and is given by , where  and are the length of the magnetic-field region traversed by the neutrons and the neutron velocity, respectively (see here for a detailed derivation of Larmor precession).

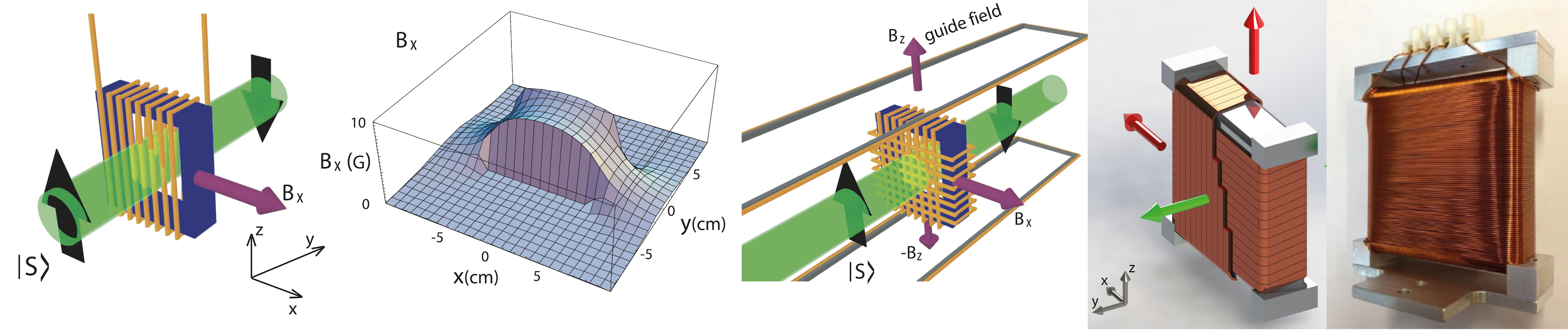
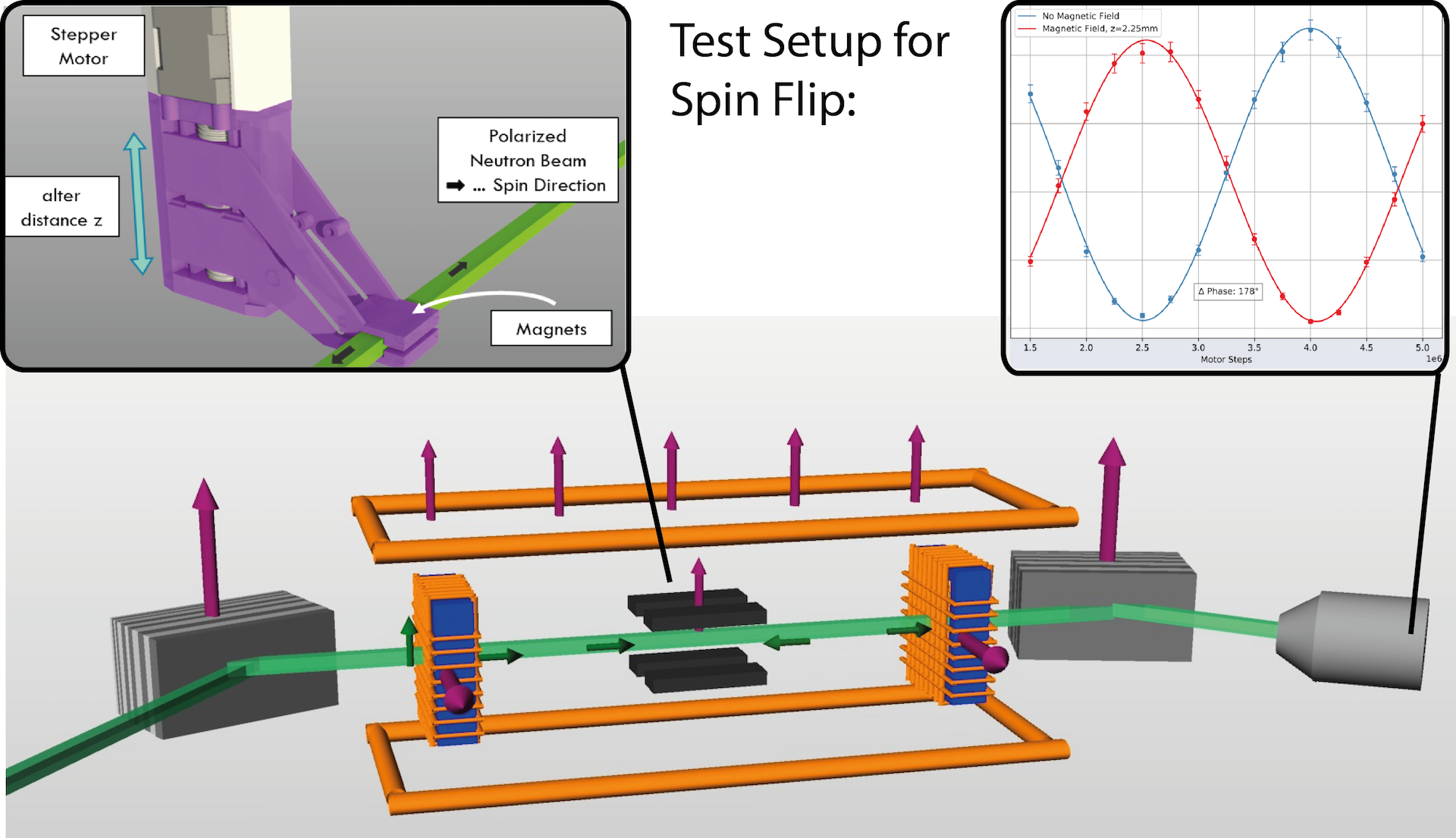
Larmor precession is often utilized in co called  Direct Current (DC) spin-rotators, or spin-flippers (if the spinor rotation angle is set to 180 deg), which is depicted below. The illustrated field configuration assures a highly non-adiabatic transit required for Larmor precession. In practice a second coils (-direction), perpendicular to the original coil (-direction) is necessary to compensate the field component of the guide field (-direction).

Using the formalism of quantum mechanics, a spin rotation through an angle  about an axis pointing in direction  is described by the unitary transformation operator , which can be written as (see here for a detailed derivation of the unitary transformation ). Note that for a stationary magnetic field the total energy of a neutron is indeed a conserved quantity since . Thus, neither the momentum nor the potential (Zeeman magnetic energy) is a conserved quantity due to and , which is depicted below (left).

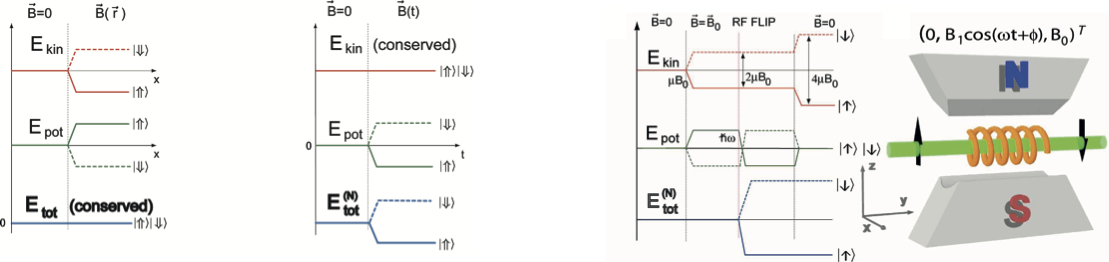
In a purely time dependent magnetic field the total energy of a neutron is not a conserved quantity: . Energy can be exchanged with the magnetic field via photon interaction. However the momentum is conserved , since due to the fact that is purely time dependent. Therefore the change in the total energy must origin from the potential energy . A diagram of the kinetic, potential and total energy is shown above (right) ¹.

An oscillating RF field and a static magnetic field—a configuration used in nuclear magnetic resonance (NMR)—is also capable of spin flipping. An oscillating RF field can be viewed as two counter-rotating fields. In the frame of one of the rotating components, the other is rotating at double-frequency and can be neglected (rotating-wave approximation). The static field component of magnitude is fully suppressed in the case of frequency resonance, i.e. for the oscillation frequency . If, in addition, the amplitude-resonance condition — determining the amplitude of the rotating field — is fulfilled, a spin flip occurs. A consequence of the rotating-wave approximation is the so-called Bloch–Siegert shift, which gives rise to a correction term for the frequency resonance now reading . The above-explained combination of static and time-dependent magnetic fields is exploited in Radio Frequency (RF) flippers, as depicted in below (see here for detailed calculations).

Next generation (3D-printed) Spin Rotators

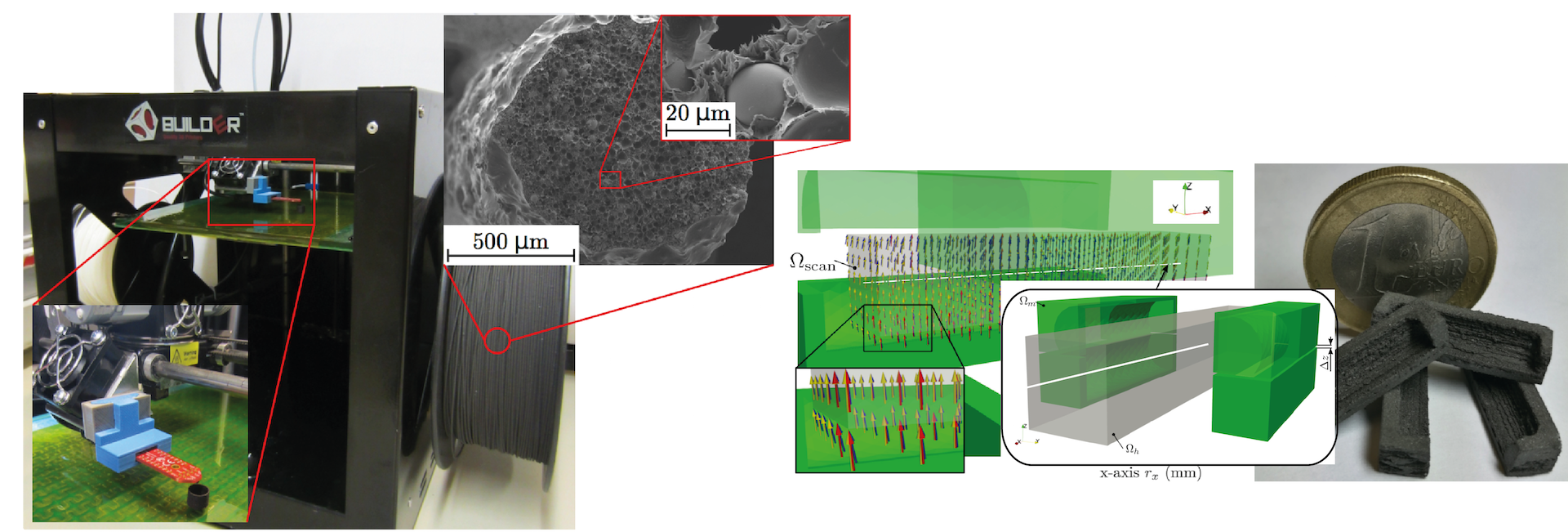
A recent projects originates in a cooperation with the group of Dieter Süss (Physics of functional materials) from the faculty of physics, university of vienna where they operate a Christian Doppler lab. This particular group demonstrated recently that an end-user 3D printer can be used to print polymer-bonded rare-earth magnets with a complex shape. A Fusing Deposition Modeling (FDM) 3D printer with a maximum temperature of 260°C, and a nozzle diameter of 0.4 mm is used to print magnetic structures with layer heights between 0.05 and 0.3 mm. The polymer-bonded magnetic compound consists of PA11 and magnetically isotropic NdFeB powder MQP-S-11-9. This source material is compounded and extruded into suitable filaments in the desired ratio of 85 wt.% MQP-S-11-9 powder.  As example of an optimized permanent magnetic system a Larmor-spin rotator for a polarized neutron interferometer setup was 3D printed.

Polarizer/Analyzer: Multi-Layer Supermirrors

For understanding the mode of operation of the applied neutron polariser we have to recap some basic concepts of of neutron optic such as the refraction index. The time dependent Schrödinger equation , with yields . See here for a detailed table of neutron scattering lengths. From the strong (nuclear) interaction of the neutron we have the Fermi Pseudopotenital denoted as 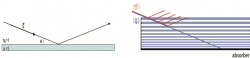, with the coherent scattering length an the atom number density ( denotes the position of each scattering center). From the magnetic interaction the contribution is given by , with , where is the magnetic moment of the neutron. So for materials containing Fe, Ni, or Co we have for the index of refraction . Since can become complex, which accounts for absorption or incoherent scattering. In general we have < 1 so the potential is repulsive with . For neutrons vacuum () is an optically denser medium compared to most elements – neutrons move in almost all materials! Hence, neutron are totally reflected, if . With and we get and a critical angle , which is depicted on the left side. For example Ni has a critical angle of 0.1°/Å. The polarizer and analyzer (spin filter) consist of multilayer structure of two media and  having different coherent scattering length . For an incident angle at every single boundary layer there will occur a transmitted an a reflected sub beam. If the thickness of the layers is chosen in such way that the partial waves of the reflected sub beams have a optical path difference of  constructive interference will be observed. If the thickness of the layers varies only slightly, from layer to layer, there will be an appropriate “lattice constant” for a diversity of wavelengths. If alternating a magnetic and a non-magnetic medium is utilized not only the nuclear scattering length, but also the magnetic scattering length has to be considered . This can be used for beam polarization, since the sign of the magnetic scattering length depends of the orientation of the spin towards the magnetization of the medium. If a combination is chosen such that the sum of the nuclear scattering length and the magnetic scattering length for one spin component (for instance ) equals the scattering length of the non-magnetic substance, then this spin component will not be reflected, since there is no difference in the refractive index of the two layers for this spin component. However, the other spin component () will be (partly) reflected. The transmitted spin component ( ) is absorbed after the last layer. An arrangement as discussed here is referred to as supermirror, often used as polarizer or analyzer ^2,3. A multilayer composed of layers whose thicknesses are varied gradually layer by layer reflects neutrons with a wide wavelength range. The thicknesses of a layer thereby vary between 5 and 35 nm and the number of layers can be several thousand. A Supermirrors are usually characterised by its critical angle as   which can go up to  .

1. F. Mezei, Physica B (Amsterdam) 151, 74 (1988). ↩

2. F. Mezei, Commun. Phys. 1, 81 (1976). ↩

3. F. Mezei and P. A. Dagleis Commun. Phys. 2, 41 (1977). ↩