November 29, 2016
Published by Stephan Sponar
Orbital Angular Momentum
Quantum Mechanical (QM) Orbital Angular Momentum (OAM) is an azimuthal phase structure imprinted on a QM wavefunction. All azimuthal structures can be described using superpositions of the OAM basis functions, , where an integer, is directly linked to the OAM along the flight path of a free particle. OAM is therefore a discrete QM degree of freedom. Three QM degrees of freedom have been identified in free neutrons: energy, position/momentum and spin. The addition of a fourth degree of freedom such as OAM would open up new avenues for experiments exploring quantum information and contextuality.
 February 7, 2025
Published by Stephan Sponar
February 7, 2025
Published by Stephan Sponar
The Sagnac effect is seen in an interferometer, when two beams of light are sent around a closed path in opposite directions. If the path is rotated, the beams become out of phase when they reunite back at the start. If the interferometer is large enough, the rotation of the Earth can be enough to shift the phases of the two beams. The effect has also been seen for particles, including electrons and neutrons. The phase shift for neutrons is proportional to the frequency of the rotation and the orbital angular momentum (OAM) of the neutron. In our work used this phase shift to work backwards and measure the OAM of the neutron using the Sagnac effect, and the rotation of the Earth. On the Larmor instrument at ISIS, we used a spin echo interferometer to produce entangled neutrons, with any path dependent phase shift detected in changes to the neutron spins. Finally, we were able to measure the OAM to within 5% of its theoretical value. N. Geerits et al. Physical Review Research 7, 013046 (2025)
(13. Jan 2025)
 January 9, 2025
Published by Stephan Sponar
January 9, 2025
Published by Stephan Sponar
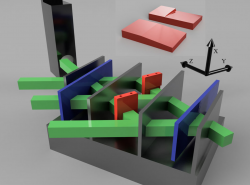
Neutron Orbital Angular Momentum (OAM) is an additional quantum mechanical degree of freedom, useful in quantum information, and may provide more complete information on the neutron scattering amplitude of nuclei. Various methods for producing OAM in neutrons have been discussed. In this work we generalize magnetic methods which employ coherent averaging and apply this to neutron interferometry. Two aluminium prisms are inserted into a nested loop interferometer to generate a phase vortex lattice with significant extrinsic OAM.
 January 10, 2024
Published by Stephan Sponar
January 10, 2024
Published by Stephan Sponar
In this work we propose that spin-orbit coupled states are generated in neutral magnetic spin-1/2 particles traveling through an electric field. The quantization axis of the orbital angular momentum is parallel to the electric field; hence both longitudinal and transverse orbital angular momentum can be created. Furthermore, we show that the total angular momentum of the particle is conserved. Finally we propose a neutron optical experiment to measure the transverse effect.
 February 14, 2020
Published by Stephan Sponar
February 14, 2020
Published by Stephan Sponar
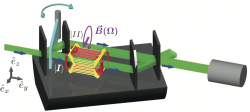
The effect of spin–rotation coupling is measured for the first time with neutrons. The coupling of spin with the angular velocity of a rotating spin turner can be observed as a phase shift in neutron interferometry and polarimetry. First a polarimeter experiment was conducted, which was later miniaturized for the actual neutron interferometric experiment. The final results agree well with the solutions acquired by the Pauli–Schrödingerequation. The observed phase shift can be attributed to geometric phase in the rotating frame of reference.
 July 15, 2019
Published by Stephan Sponar
July 15, 2019
Published by Stephan Sponar
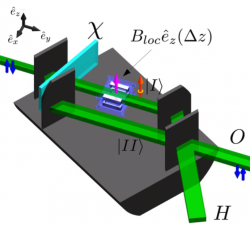
We have developed a new method for coherent Larmor spin-rotation control using topology optimized 3D printed magnets for applications in neutron interferometer experiments, where the rotation axis is parallel to the outer guide field. The magnetic action can be adjusted linearly by varying the distance between the magnets. We have showed that spin-rotation angles of more than 4 are possible, depending on the initial magnetization strength. The advantages of this new method are that unwanted inductances are avoided, and that no heat is dissipated by current carrying wires, which prevents a reduction in interferometric contrast due to temperature gradients or would make water cooling necessary.




