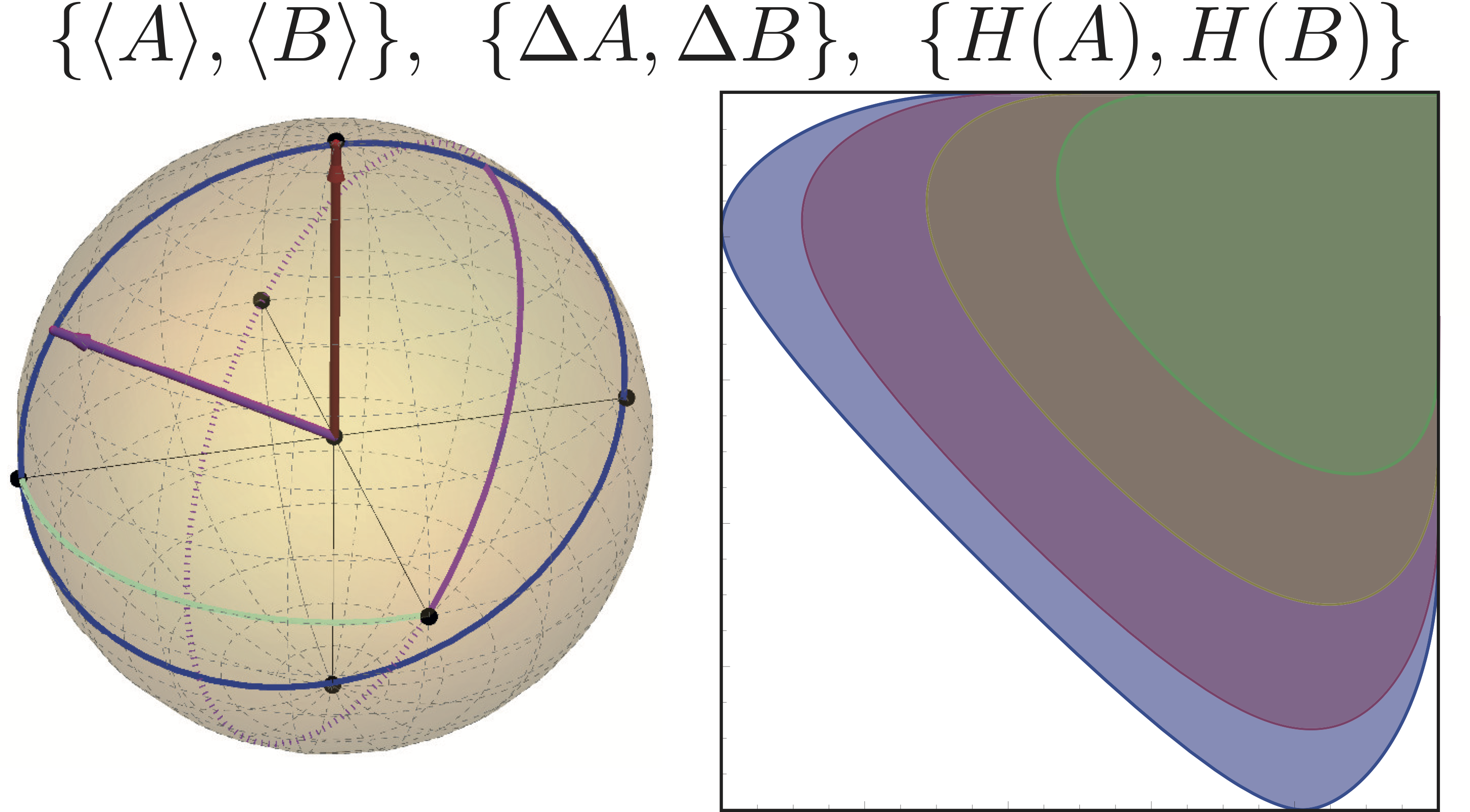
Tight State-Independent Preparation Uncertainty Relations for Qubits

In our polarimetric experiment ¹ we study tight state-independent preparation uncertainty relations for quits, as proposed by Abbott et al in ². The recent interest in measurement uncertainty relations revealed that the well-known Robertson-Schrödinger uncertainty relation lacks an irreducible or state-independent lower bound. Abbott et al., proposed a state-independent tight preparation uncertainty for arbitrary Pauli observables and , where every quantum state satisfies the condition .

The standard deviation and expectation value are connected via and , since every Pauli operator satisfies . Hence, the tight state-independent uncertainty relations from above can be rewritten in terms of standard deviations as . Busch et al. proposed two state-independent uncertainty relations for  two-level systems (qubits), expressed as and  in 2014 ³ . However, these relations are not tight in general.

In the case of qubits, the Shannon entropy of a Pauli observable can be directly expressed in terms of the expectation value , namely: , where is the binary entropy function defined as , or with , where denotes the inverse function of . Then one obtains the following tight relation for two Pauli observables . This entropic state-independent uncertainty relation is tight, unlike those of Deutsch ⁴ from 1983 , or the well-known Maassen and Uffink ⁵ relation , with .

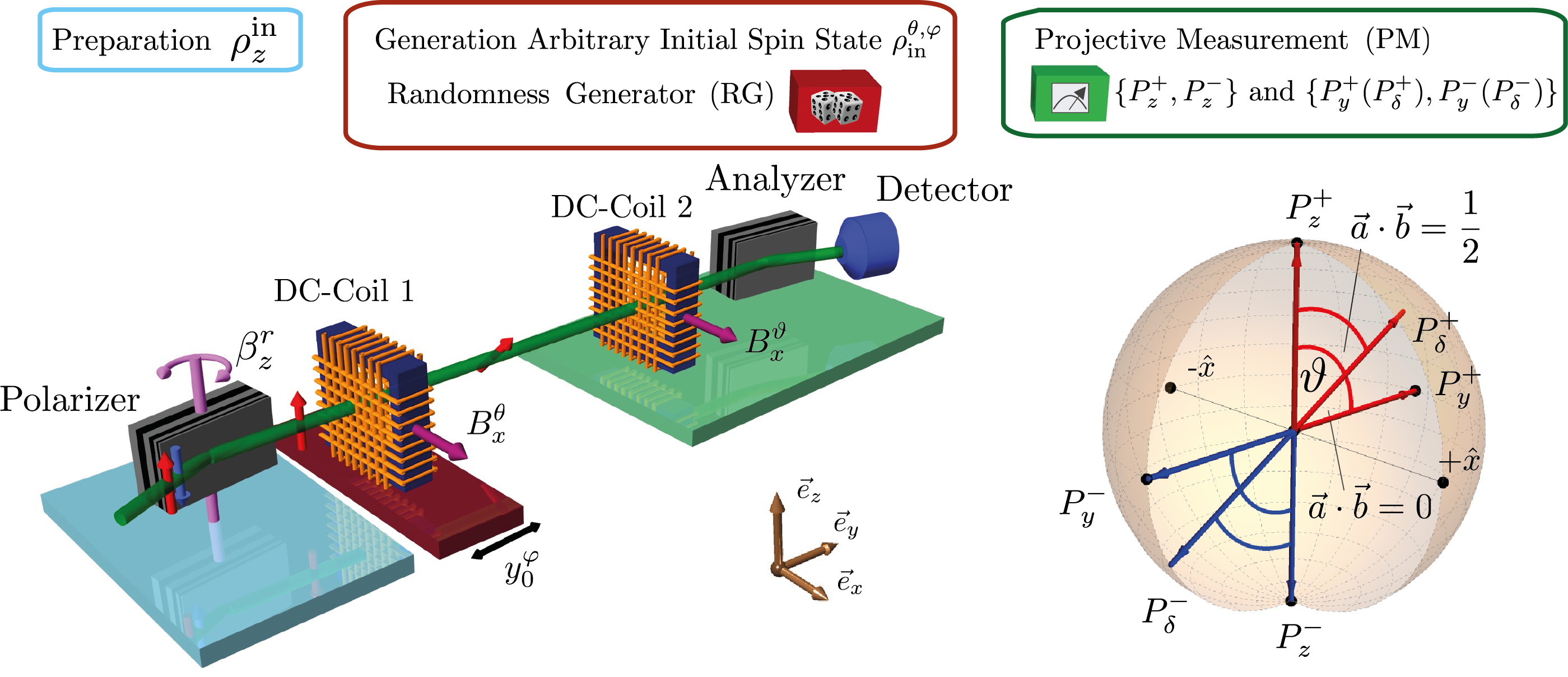
We investigate (i) and (ii) . For (i) we chose and , thus the four projectors and were measured for every randomly chosen initial state , resulting in an observed intensity denoted as , with and . The setup is illustrated below: projectors are realized by the action of the supermirror (analyzer) while applying the respective magnetic fields in DC-coil 2. Inside DC-coil 2, the magnetic field induces spinor rotations of and about the x-axis, required for projective measurements along the +z,-z,+y and -y-direction, respectively. Since all four projectors lie in the y-z-plane the position of DC-coil 2 remains unchanged. For (ii) , which corresponds to an angle of deg between and , we have again but now. The respective projectors are denoted as and , respectively and depicted on the Bloch sphere below.

Relations for pure states

The lowest or state-independent bound, expressed by the very RHS Abbott’s relations, for expectation values, standard deviations and entropies, respectively, is saturated for pure initial states (r=1), which will be studied first.

i) Orthogonal observables

Two Pauli observables and , with and , yielding , are selected (see Bloch sphere below).

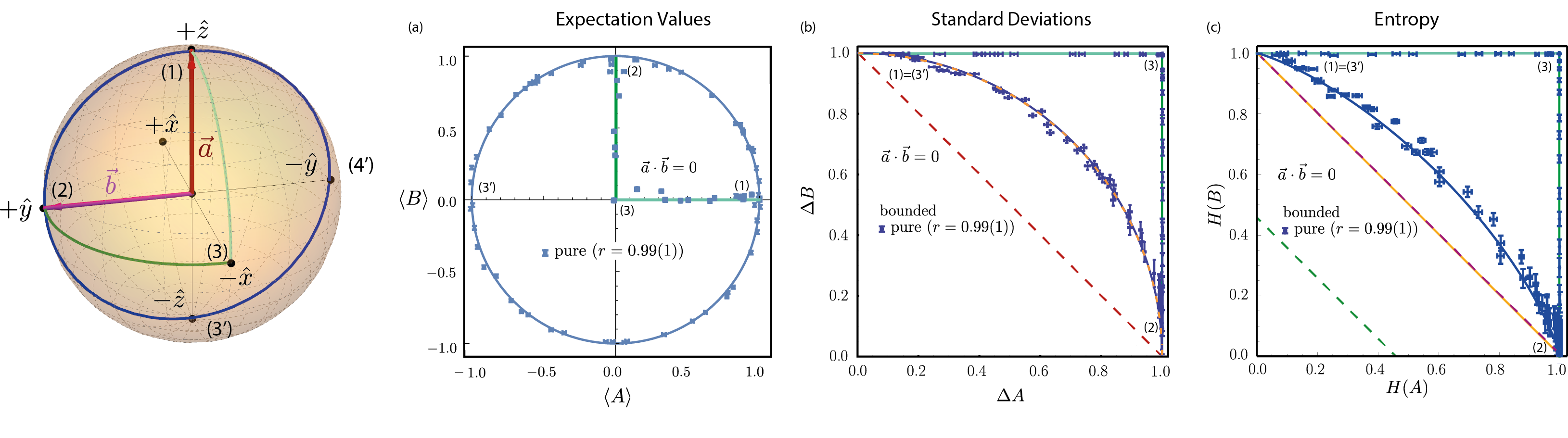
Plots of the experimentally obtained values for Pauli observables , in terms of expectation values , , standard deviations , (including bounds from Busch dotted red line and dashed orange curve), and entropies , (including bounds from Deutsch dotted green line, Maassen, Uffink dashed violet line. Blue curves (same as dashed orange curve) indicate the theoretic predictions of lower bounds for expectation values, standard deviations and entropies, respectively. Dark green line (connecting points (1) – (3)) and light green line (connecting points (2) – (3)) represent the theoretic predictions for values of the corresponding initial states indicated by the respective color (points) on the Bloch sphere.

ii) Non-orthogonal observables

Next, expectation values, standard deviations and entropies for Pauli observables and , with , which corresponds to a relative angle \,deg (see Bloch sphere below), are investigated.

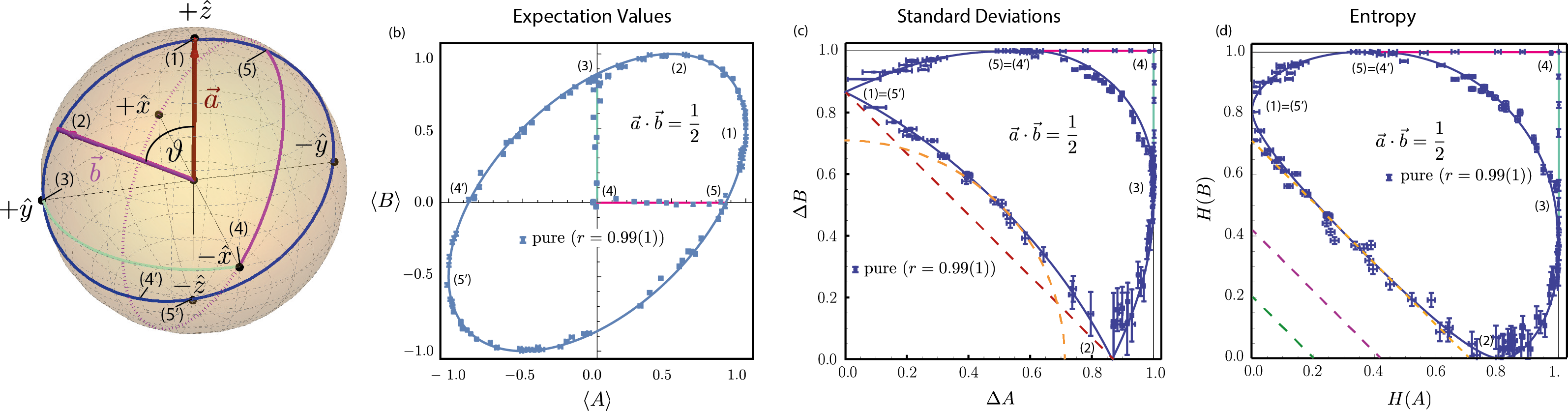
Plots of the experimentally obtained values for Pauli observables , in terms of expectation values , , standard deviations , (including bounds from Busch dotted red line and dashed orange curve), and entropies , (including bounds from Deutsch dotted green line, Maassen, Uffink dashed violet line. Blue curves (same as dashed orange curve) indicate the theoretic predictions of lower bounds for expectation values, standard deviations and entropies, respectively. Dark light green line (connecting points (3) – (4)) and magenta line (connecting points (4) – (5)) represent the theoretic predictions for values of the corresponding initial states indicated by the respective color (points) on the Bloch sphere.

Relations for mixed states

As already discussed above, the state-independent bound , is saturated only by pure states, found on the surface of the yz-plane on the Bloch sphere. The partially state-dependent lower bound, expressed as , is covered by mixed states located in the yz-plane of the Bloch sphere, with respective degree of polarization r. For expectation values the lower bound is a closed curve representing the entire boundary of allowed values for and , which can be seen in plots below for (orthogonal case) and (non-orthogonal case), respectively. The measurement is carried out for three initial degrees of polarization, which are tuned by the angle between the supermirror and the neutron beam, namely , and .

i) Orthogonal observables

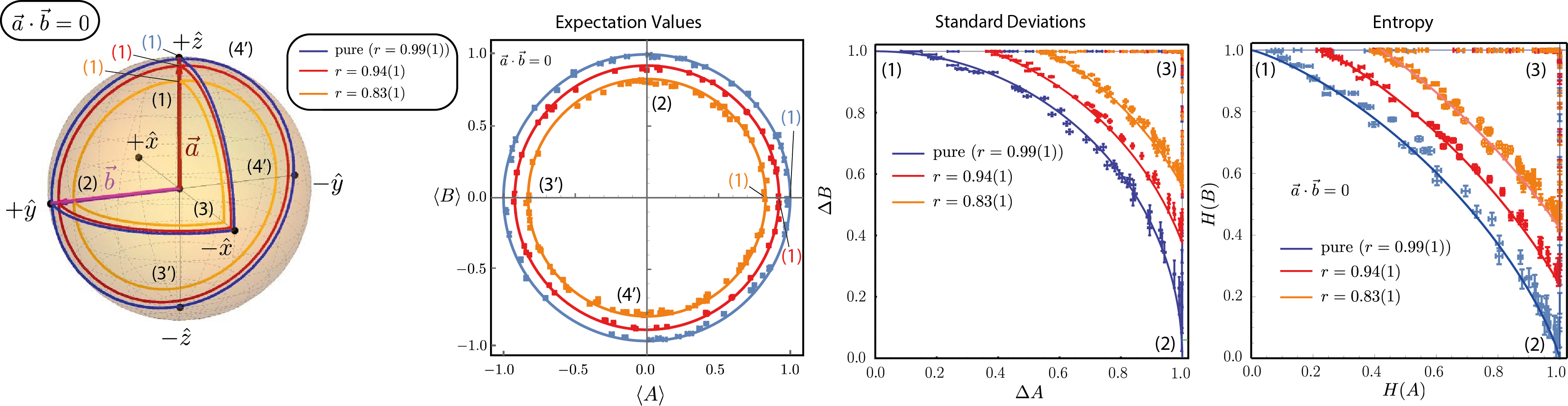
Plots of the experimentally obtained values for Pauli observables , in terms of expectation values , , standard deviations , , and entropies , for , and .

ii) Non-orthogonal observables

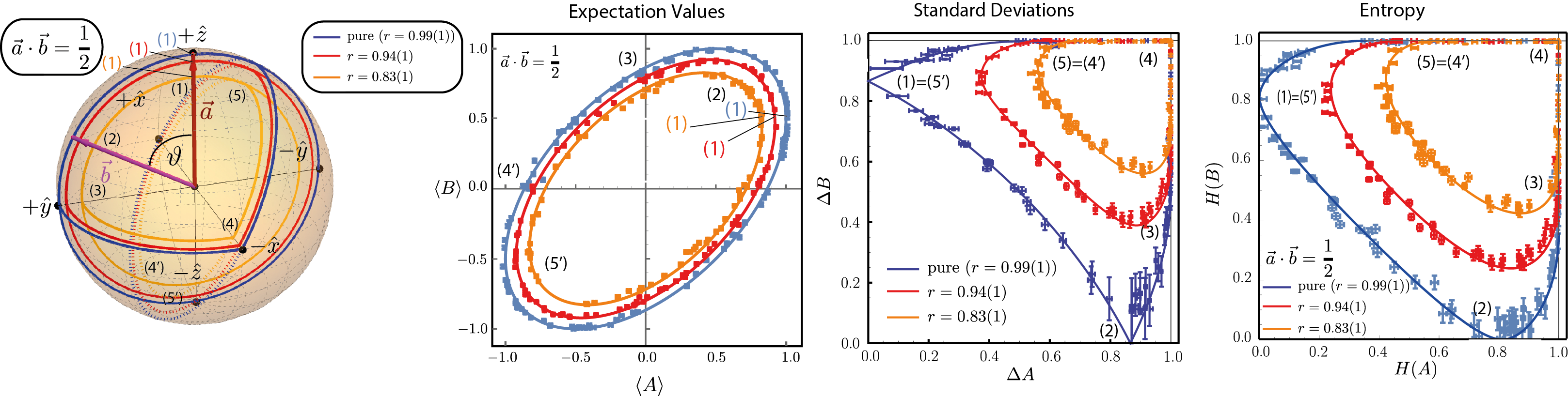
Plots of the experimentally obtained values for Pauli observables , in terms of expectation values , , standard deviations , , and entropies , for , and .

To summarize; the presented experiment investigates the relationship between the expectation values of Pauli spin observables and two standard measures of uncertainty, namely standard deviations and Shannon entropies. The tightness of state-independent  uncertainty relations for Pauli measurements on qubits is experimentally demonstrated. In addition, we observed bounds on these relations, expressed in terms of the norm  of the Bloch vector, resulting in (partially) state-dependent uncertainty relations with lower bounds. We have experimentally confirmed the tightness of state-independent, as well as partially state-dependent, uncertainty relations for pairs of Pauli measurements on qubits. The observed uncertainty relations, expressed in terms of standard deviations and Shannon entropy (both functions of the expectation value), completely characterize the allowed values of uncertainties for Pauli spin observables.

1.  S. Sponar, A. Danner, K. Obigane, S. Hack, and Y. Hasegawa, Phys. Rev. A 102, 042204 (2020). ↩

2. A. A. Abbott P-L Alzieu, M. J. W. Hall and C. Branciard, Mathematics 4, 8 (2016). ↩

3. P. Busch, P. Lahti, and R. F. Werner Phys. Rev. A 89, 012129 (2014). ↩

4. D. Deutsch, Phys. Rev. Lett. 50, 631 (1983). ↩

5. H. Maassen and J. B. M. Uffink, Phys. Rev. Lett. 60, 1103 (1988). ↩