Experimental Test of Information-Theoretic Measurement Uncertainty Relation for general Qubit Observables

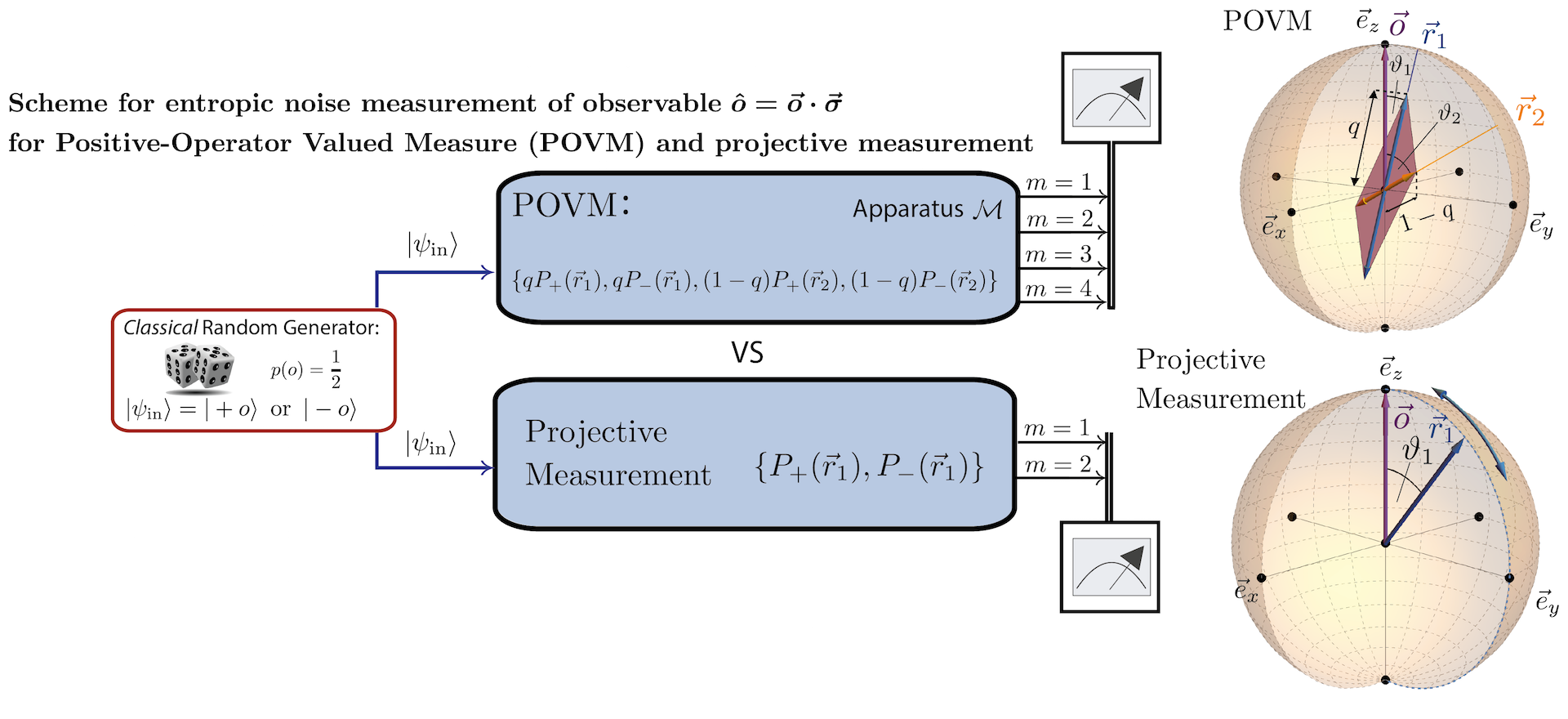
In our optical experiment ¹ we test noise-noise trade-off relations for variouse Pauli observables by implementing four-outcome positive-operator valued measure POVMs (see here for details of POVMs), as proposed in ². Details of the theoretical framework can be found here. Our results confirm that POVM measurements outperform projective ones and allow for an experimentally saturation of a tight qubit uncertainty relation. Below an illustration of the applied four output POVM expressed as , where , and the are unit vectors on the Bloch sphere parametrized by the spherical coordinates with . For the POVM reduces to a single projective spin measurement along the direction , which is depicted below. On the other hand for a value of between and it corresponds to a mixture of projective measurements along the directions and with probabilities and .

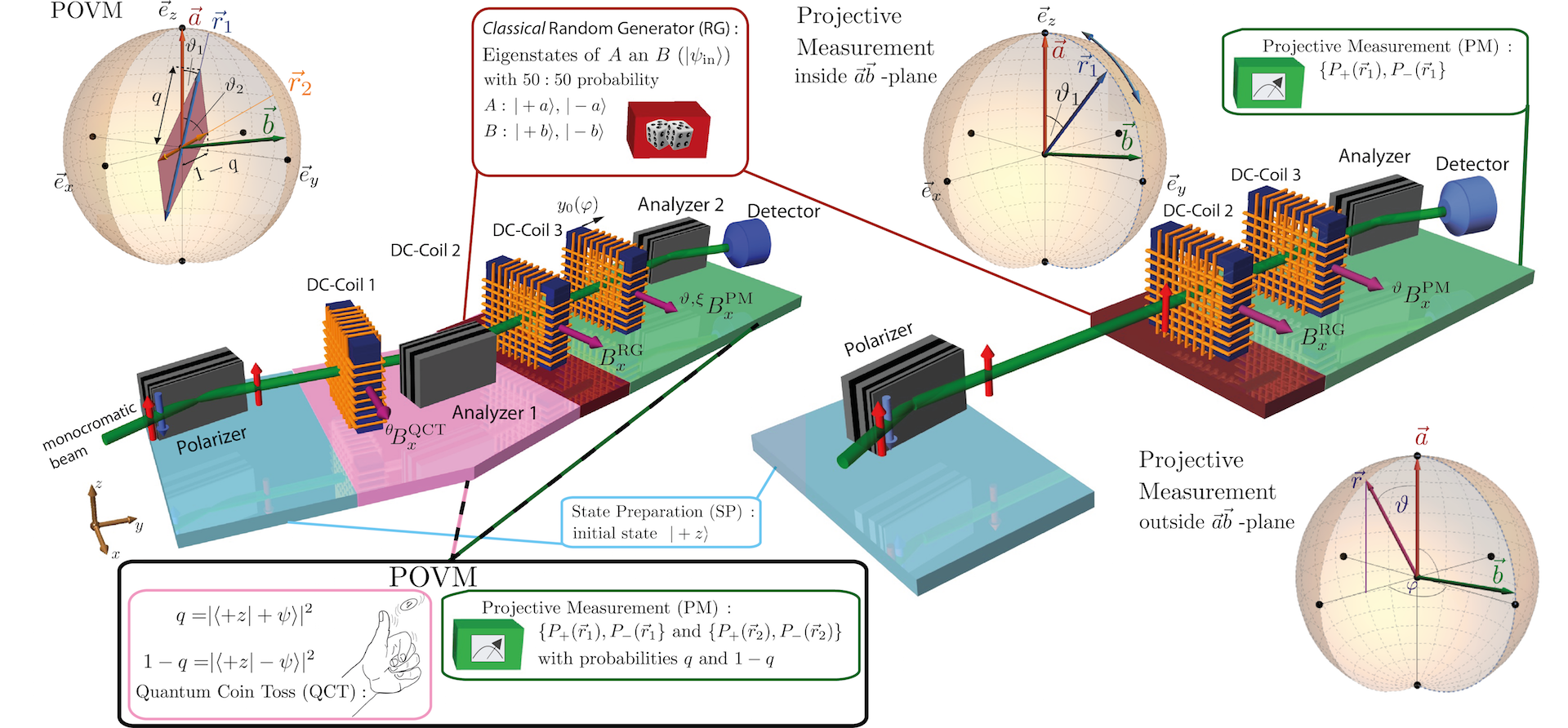
Experimentally the POVM is realized the following way: after the initial State Preparation (SP) of , the initial spins are rotated by DC-coil~1 (see setup in setup below) before being transmitted through Analyzer 1 with probabilities depending on the incident angle of spin states , which we refer to as Quantum Coin Toss (QCT). The respective setup is depicted below left. For  the scheme reduces to a single projective spin measurement along the direction  , the setup for this simpler scenario is depicted below right (note that one coil and one analyzer are missing since the QCT becomes obsolete). Behind Analyzer 1, one of the observables’ eigenstates or (with eigenvalues ) is generated uniformly by DC-Coil 2 using a Classical Random Generator (RG). Finally,  DC-Coil 3, together with the last analyzer performs the projective measurement of or  (or just for the projective measurement alone). Details of the data analysis can be found here.

The final results results for three different vectors are given below.  Very left: we have   being non-convex, more precisely  . Here, the projective measurement is clearly suboptimal. The optimal values are obtained via POVMs with different  values measured along directions starting from  () and (). The shaded noise-noise regions are split in two areas: The orange area indicates values that cain only be obtained by POVMs. The purple area can be reached by projective measurements. Blue data points are measured in the -plane starting from () and increasing in steps of along  . Finally the purple points are obtained by projective measurements  out of the -plane by increasing the azimuthal angle . Second from left: For   (which corresponds to a relative angle of between the observables; still non-convex)  the lower boundary (orange) and, more noticeably the purple region start shifting downwards. The two measurement directions for the POVM   and  now have polar angles  and . The projective measurements in the -plane are no longer symmetric and are found on a closed loop. Third from left: For   (relative angle of ) we have the transition from non-convex to convex. The dashed orange line indicates that projective measurements are theoretically incapable of saturating the noise-noise tradeoff, but improvements by POVMs are no longer resolvable in our experiment – the orange area has become a line ! Right: for  (relative angle of ) the region has now become convex and can be fully attained with projective measurements – improvements by general POVMs are here no longer possible.

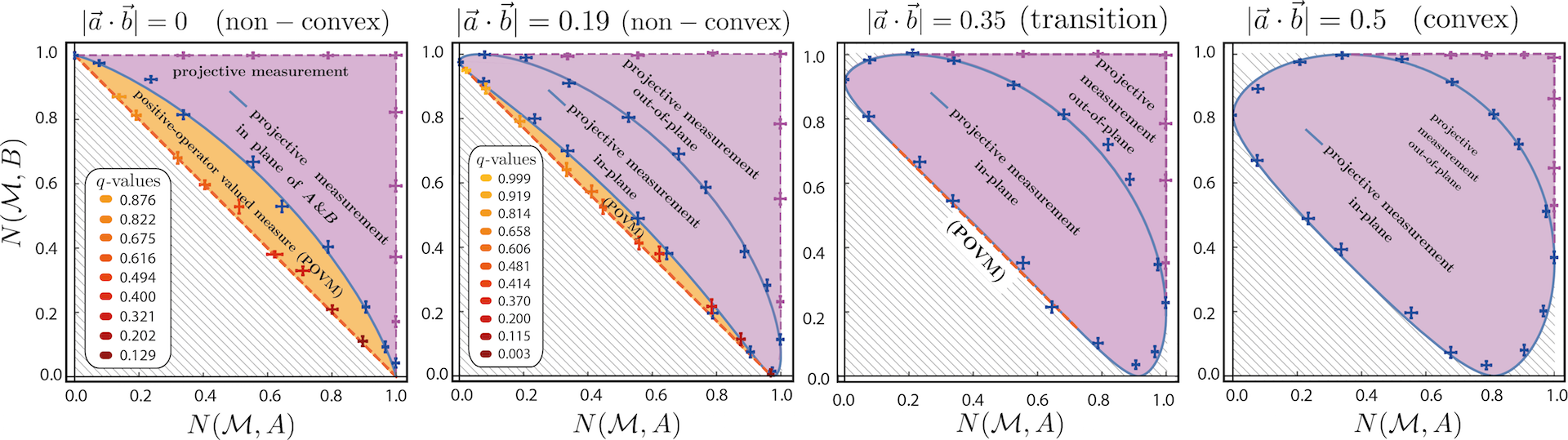
For closely aligned observables – more precisely for angles smaller than – we saw that the uncertainty relation could be saturated with simple projective measurements. However, we verified experimentally that this is not generally the case and that four-outcome POVMs yield better results that saturate the uncertainty relation when projective measurements cannot.

1. Bülent Demirel, Stephan Sponar, Alastair A. Abbott, Cyril Branciard, and Yuji Hasegawa, New J. Phys 21,013038 (2019). ↩

2. Alastair A. Abbott, Cyril Branciard, Phys. Rev. A 94, 062110 (2016). ↩