A short Excursion into Crystallography

October 11, 2015 3:42 pm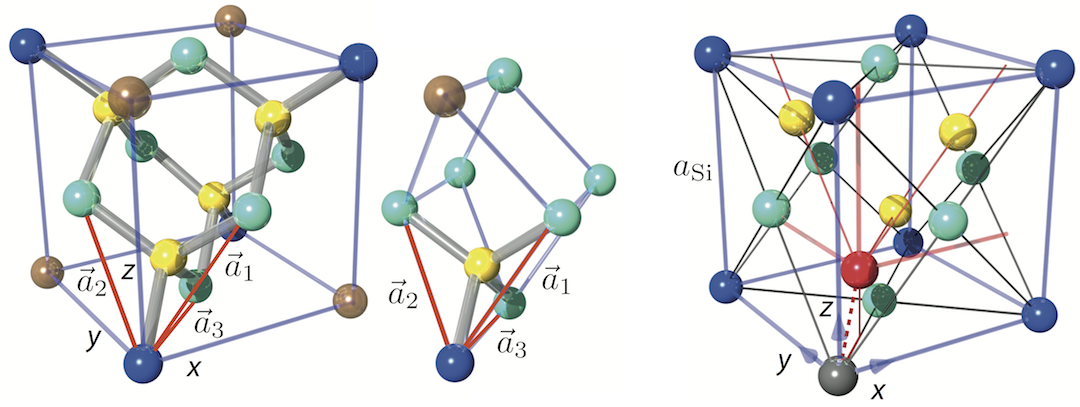 Published by Stephan Sponar

In a silicon perfect crystal each silicon atom is bonded covalently, via bonds, with other surrounding four Si atoms in a regular tetrahedral configuration. The lattice is a variation of the face centered cubic crystal structure called diamond lattice. The structure, including it’s chemical bonding, is schematically illustrated below left. Four atoms (yellow) are bonded to four others within the volume of the (cubic) conventional unit cell. Six atoms fall on the middle of each of the six cube faces, showing two bonds (light blue). Out of eight cube corners, four atoms bond to an atom within the cube (dark blue) and four are bonded outside of the cube (light brown), altogether 18 Si atoms. The primitive cell, depicted in the middle, consist of three lattice vectors given by , , and . The lattice constant of silicon is roughly =5.43 Å.

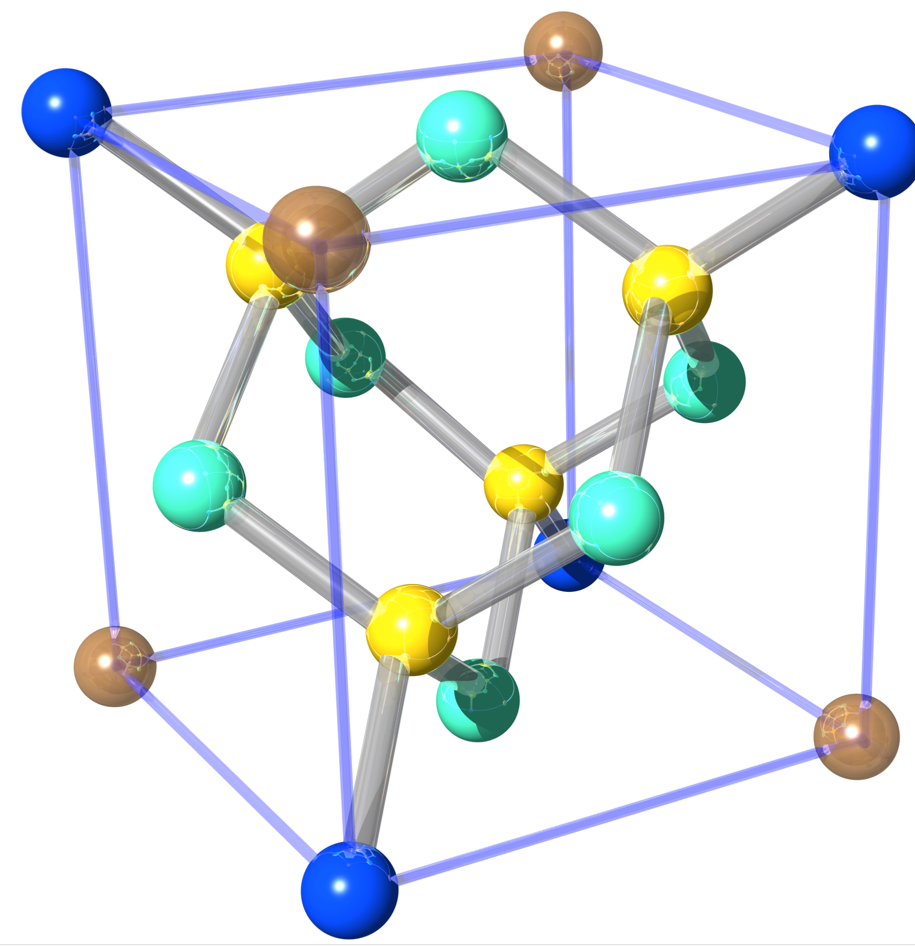
Silicon’s crystallographic structure, as mentioned before, is diamond cubic, which is in the Fdm space group, following the face-centered cubic Bravais lattice. The conventional unit cell, depicted above right, consists of two basis atoms and may be thought of as two inter-penetrating face centered cubic lattices, with a basis of two identical Si atoms associated with each lattice point one displaced from the other by a translation of () along a space diagonal (indicated by the dotted red line). We start with the gray colored Si atom sitting in the origin of the cell and the second is the red colored Si atom. The seven remaining corners are colored in dark blue (note that in this illustration the colors have different meanings). In light blue we have the face-centered atoms of the original conventional cell and in yellow the face-centered atoms of the shifted cell (whose origin is indicated by the red coordinate system). The number of atoms in the unit cell is 8: the eight atoms at the corners belong to 8 cells, the 6 face-centered atoms to two, and four atoms are inside the unit cell. This is illustrated below for the grey Si atom at the corner (left) and face-centered (right). Thus, in total we get . From that it is easy to calculate that the silicon sphere, used in the International Avogadro Project at the National Institute of Standards and Technology (NIST) aiming to redefine the kilogram, has a radius of roughly 4.685 cm.

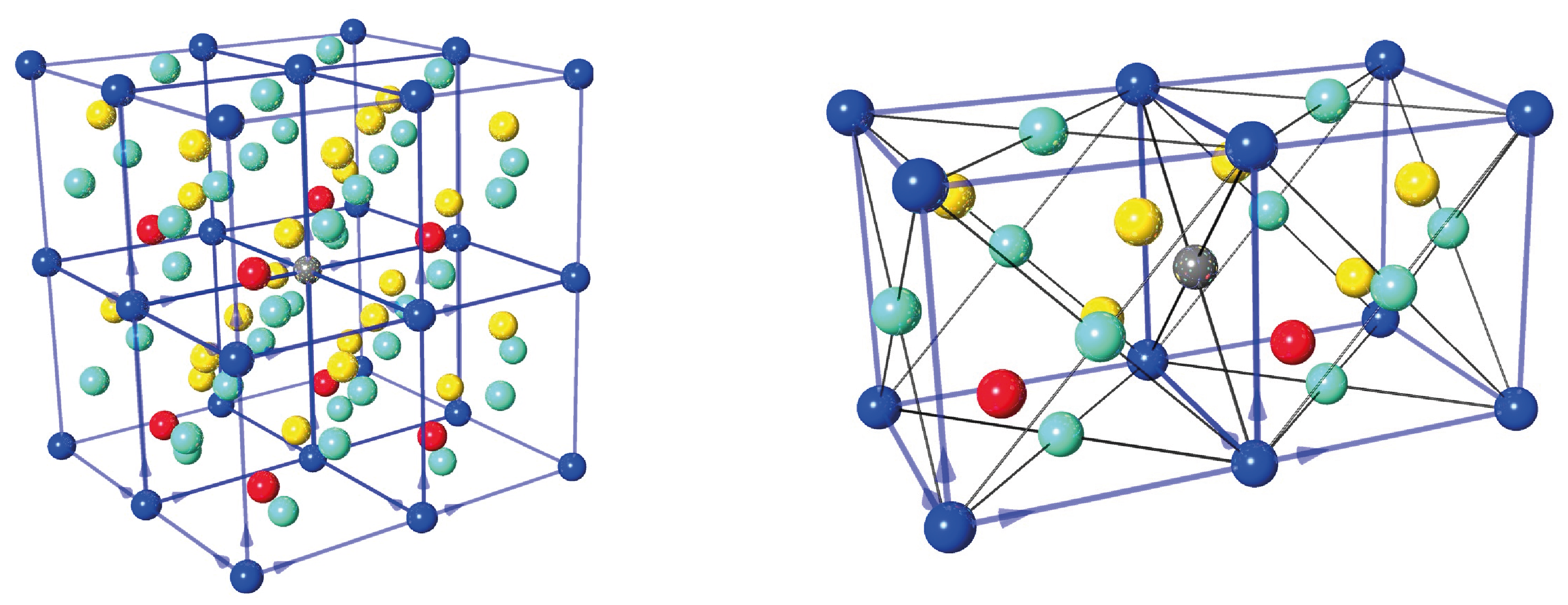
In our experiments we only use the {2,2,0} reflection, which is illustrated below left and the right (top-view). The lattice separations is calculated as Å. The reflected wavelength is given by Bragg‘s law as . Hence, the maximum wavelength is found for back-reflection () yielding Å.

On the left side of the image below you can see an image of the {111} reflection planes with Å, which is significantly larger compared to the {220} reflection. On the right side we have the {113} reflection with Å (note that the unit cell has been rotated by 90 degree for illustrative purpose).

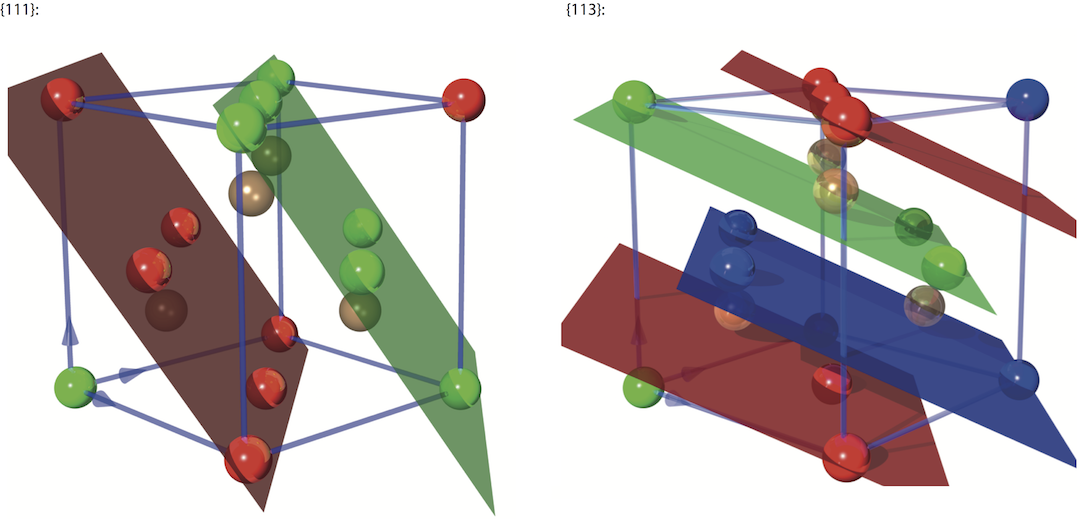
Atoms colored in brown do not belong to the particular reflection planes in the figure above. Other reflections, apart from {2,2,0}, {1,1,0}, {111} and {113}, that are also used in neutron optics are formed by the {115}, {117}, {331}, {335}, and {551} lattice planes.