The Interferometer – a Two-Level System

Considering a conventional Mach-Zehnder interferometer in which the beam-pair spans a two dimensional Hilbert space . The state vectors and are as wave packets that move in two given directions defined by its vector owing to the geometry of the interferometer. In accordance with the nomenclature in dynamical theory of diffraction they are reffered to as   and  . On this basis, we may represent mirrors, beam splitters, and relative phase shifts by the unitary operators , and , respectively. A pure input state is transformed after the first plate of the interferometer (beam-splitter) to . After the second plate (assumed to act as a mirror) we get . The effect of the phase shifter yields . Behind d the third plate (second beam-splitter) the state is given by . That yields, after the projection in forward (O-direction ) the intensity .

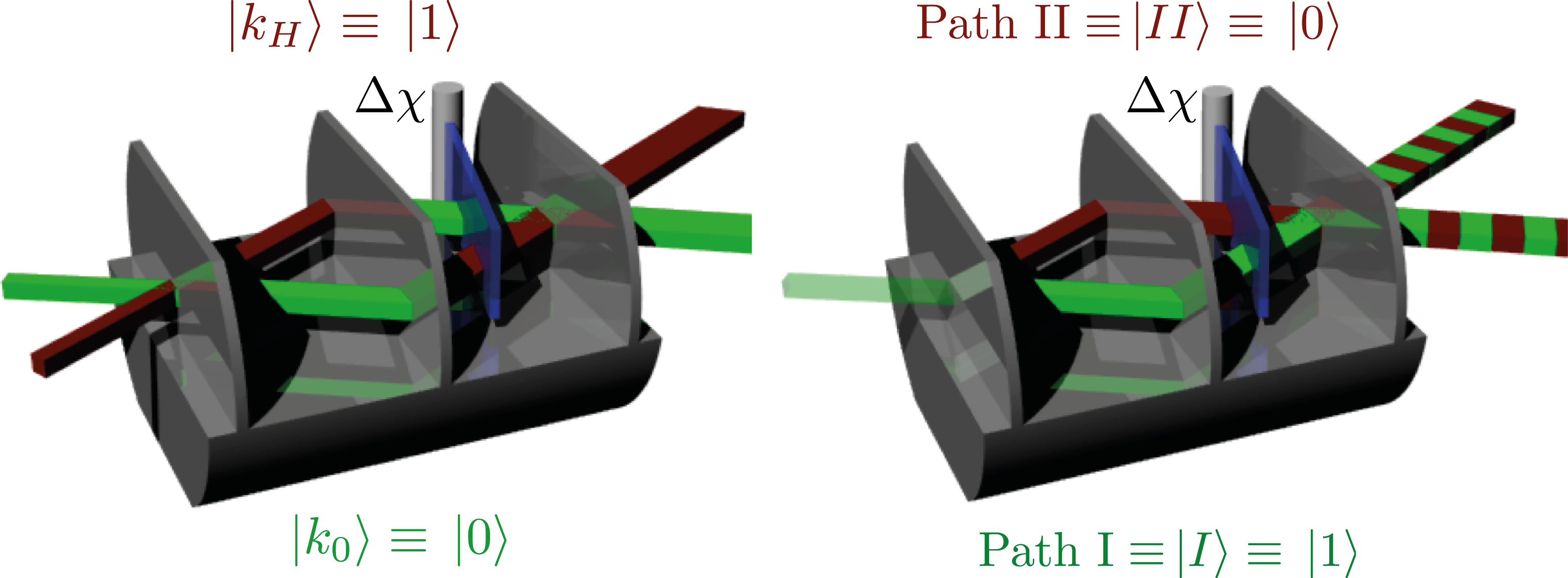
However, there is also a second more intuitive description, where the eigenstates are represented by path I and path II. Here we start right on with the superposition state . After the phase shifter we get  . At this point the descriptions start to diverge; in order to get the intensity in forward direction (O-direction) we have to apply the projector to get the the intensity .

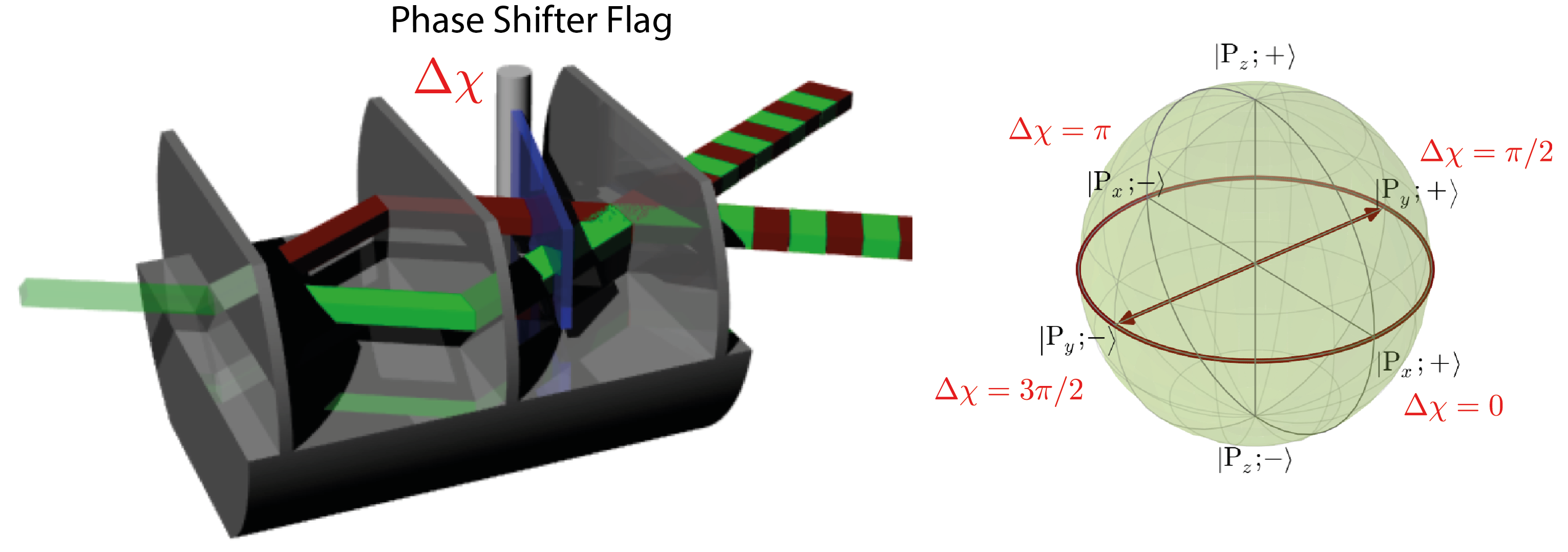
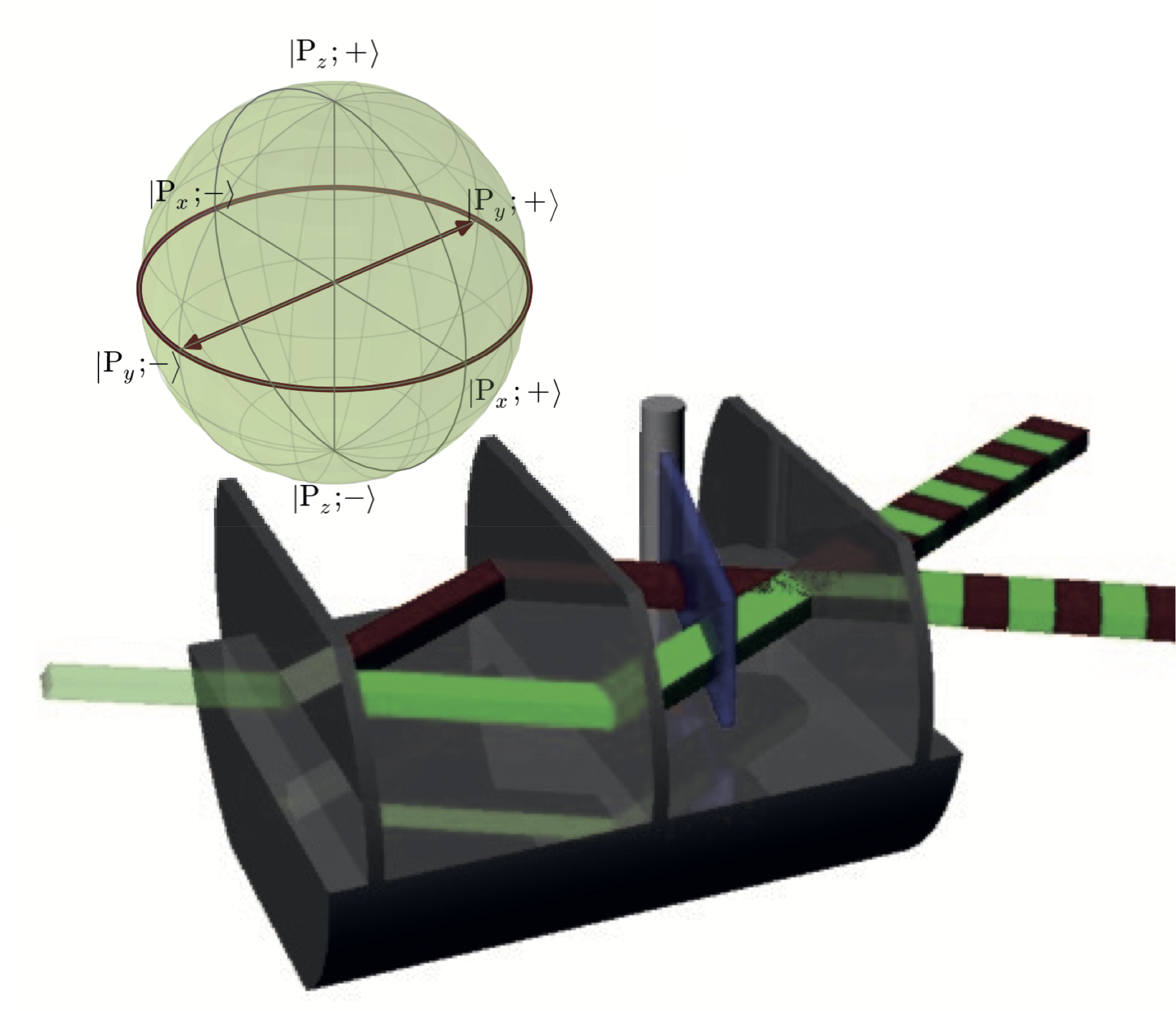
The quantum state of the neutron’s path degree os freedom is depicted on the Bloch sphere. As ecpected a equally wighted superposition state is found on the equatorial plane of the Bloch sphere and the azimuthal angle is defined by the relative phase between the path eigenstates, which is illustrated above for and  directions, together with the respective (phase) values of .