Bell’s Inequality Experiments

Quantum entanglement is a physical phenomenon that occurs when two (or more) quantum systems are generated (prepared) in such a way, that the quantum state of individual (sub) system cannot be described independently – even when the systems are separated by a large distance. Measurements of physical properties of the individual (sub) systems on entangled quantum system are found to be appropriately correlated. Such phenomena were the subject of a 1935 paper by Albert Einstein and his co-authors Boris Podolsky and Nathan Rosen (EPR) ¹, which made the authors state that quantum mechanic was incomplete, arguing that a more complete, deterministic hidden physics must underly quantum mechanics (see here for details on the EPR thought experiment). Such a theory should be supplemented by additional, so called hidden variables, addressing objective properties (elements of reality) of physical systems in order to restore causality and locality. Quantum entanglement is a major resource in quantum computation and quantum communication, an area of extremely active research by the physics community (see here for details on hidden variables). In 1951 David Bohm reformulated the EPR argument for spin observables of two spatially separated entangled particles to illuminate the essential features of the EPR paradox. It took more than a decade, till late 1964 when  John Stewart Bell ² introduced inequalities for certain correlations which hold for the predictions of any hidden-variable theory applied. Using these co-called Bell inequalities entanglement has been verified in various quantum systems ³, first for photons, and later just to mention neutrinos, electrons, (very large) molecules, (small) diamonds, and by us with neutrons ⁴.

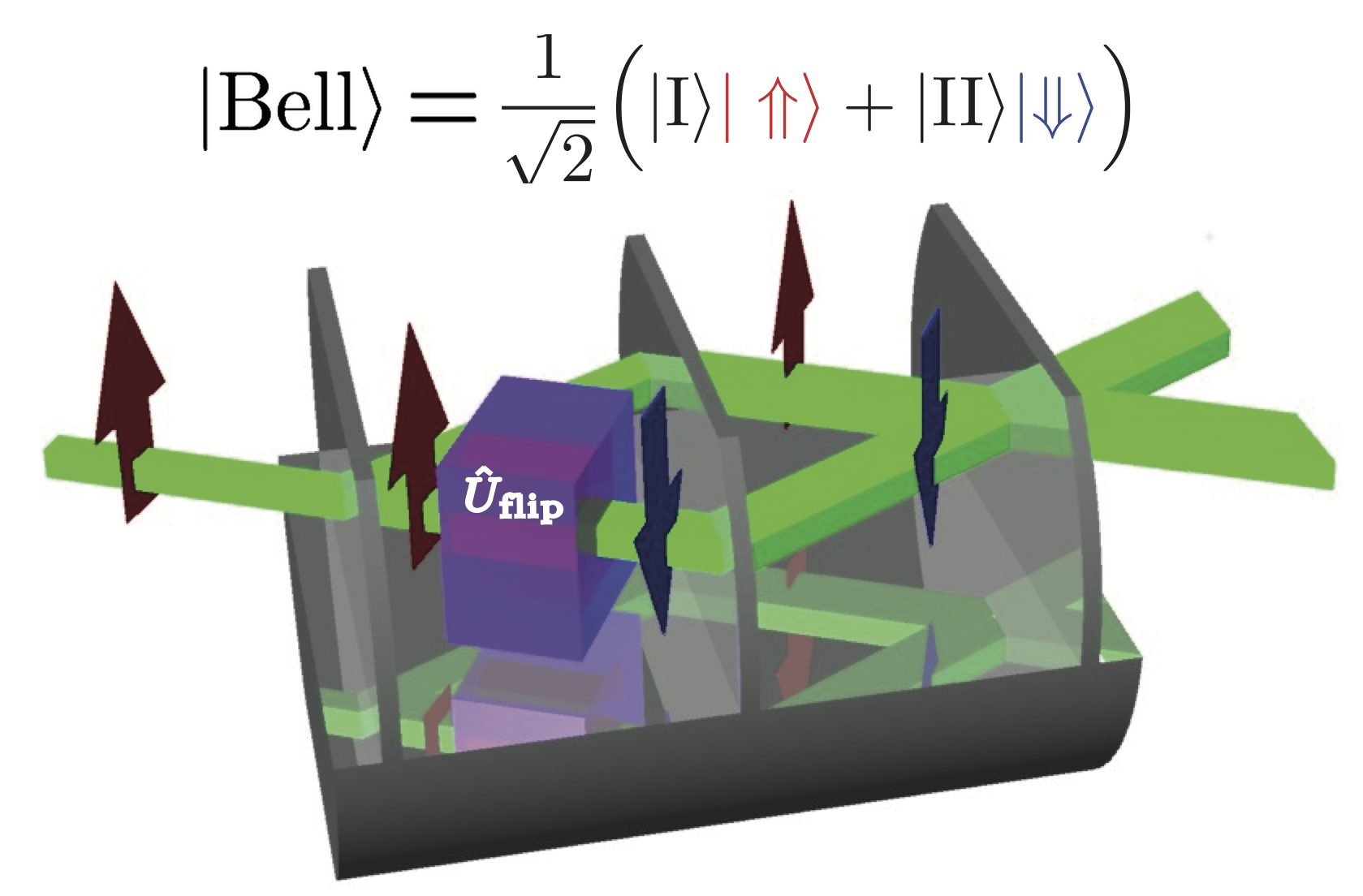
Entangled Quantum State (EQS) preparation: (left) for two photos via parametric down-conversion in a beta-barium borate (BBO) crystal. (right) for a single neutron by a spin flip in one of the two paths in a triple Laue (LLL) neutron interferometer.

In the case of neutrons, entanglement is achieved between different degrees of freedom (intra-particle entanglement) of the single particle system and not between individual particles (inter-particle entanglement), as it is the case for example in photonics systems. Each individual degree of freedom (DOF) is described formally as a two-level system. One example of such intra-particle entanglement is an entangled state of the neutron spin and path DOF in neutron interferometry. When the incident beam is polarized, the spin in one path of the IFM can be flipped and the neutron wavefunction exhibits entanglement between the spinor and spatial parts, which is schematically illustrated in the figure above. The corresponding state vector is a maximally entangled Bell state, given by . A picture of the experimental setup and a schematic illustration of the neutron optical devices is given below panel (a).

(a) Schematic view of the entire interferometric setup. (b)Larmor accelerator boxes with coils in Helmholtz geometry (yellow), magnetic field (red), neutron beam (green) and water flux (blue), (c) Larmor acceleration coil with Helmholtz geometry in box, (d) closed box with connectors for water cooling, and (e) boxes in the interferometer with connected cooling system and absorber holder for adjustment of the setup.

For precise measurements with polarised neutrons high efficient spin-manipulation is required. We developed several neutron optical elements suitable for a new sophisticated setup, i.e., DC spin-turners and Larmor-accelerators which diminish thermal disturbances and depolarisation considerably, which is depicted above in (b)-(e). The gain in performance is exploited demonstrating violation of a Bell-like inequality in Clauser-Horne-Shimony-Holt (CHSH) formalism (see here for details on CHSH Bell inequalities. The obtained value of S=2.365(13), which is much higher than first measurement, where a value of 2.051(19) was obtained ⁴. The current result is   above the limit of   predicted by contextual hidden variable theories (in the first experiment only could be reached). Detailed information of the experiment is reported in  ⁵. Another interferometric Bell test, where the effect of the geometric phase on a Bell measurement is studied can be found here. In addition to Bell tests entanglement between spin and path degree of freedom has been also demonstrated by full tomographic analysis of the density matrix of the Bell state  ⁶ (see here for details), where a concurrence of 0.59(3) is clear evidence of the entanglement.

Click here for an animation of the experiment

Another intra-particle type of entanglement is spin–energy entanglement ⁷. When interacting with a time-dependent magnetic field the total energy of neutrons is no longer conserved (see here for a detailed description of the interaction of magnetic fields with neutrons). The total energy of the neutron decreases (or increases) by during the interaction with a radio-frequency (RF) flipper. This fact can be used to create a spin–energy entangled state (without need for spatial separation in a polarimetric setup) expressed as The incoming spin superposition can be created by applying a spin rotation of an initially polarized beam. and are the energy eigenstates after interaction with a time-dependent magnetic field within an RF flipper driven at frequency . All our experiment described here below to the field of bipartite entanglement. Tripartite entanglement in single-neutron interferometer experiments is explained here.

1. A. Einstein, B. Podolsky, and N. Rosen, Phys. Rev. 47, 777 (1935).  ↩

2. J.S. Bell Physics (NY) 1, 195 (1964). ↩

3. R. Horodecki et al., Rev. Mod. Phys. 81, 856 (2009); N. Brunner et al., Rev. Mod. Phys. 86, 419 (2014). ↩

4. Y. Hasegawa, R. Loidl, G. Badurek, M. Baron, and H. Rauch, Nature (London) 425, 45-48 (2003). ↩

5. H. Geppert, T. Denkmayr, S. Sponar, H. Lemmel, and Y. Hasegawa, Nucl. Instr. Meth. Phys. Res. 763, 417–423 (2014). ↩

6. Y. Hasegawa, R. Loidl, G. Badurek, S. Filipp, J. Klepp, and H. Rauch, Phys. Rev. A 76, 052108 (2007). ↩

7. S. Sponar J. Klepp, C. Zeiner, G. Badurek, and Y. Hasegawa, Phys. Lett. A 374, 431-434 (2010). ↩