Geometric Phase in entangled Systems
November 29, 2014 10:40 amThe total phase acquired during an evolution of a quantal system generally consists of two components: the usual dynamical phase which is dependent on dynamical properties like energy or time, and a geometric phase, which is, considering a spin 1/2 system, minus half the solid angle of the curve traced out in ray space.
Contents:
Berry phase for an entangled state of two spin- particles
Geometric phase in a single-neutron interferometer experiment
Berry phase for an entangled state of two spin- particles
First we give a summary of the theoretical framework as introduced in a paper by Reinhold A. Bertlmann 1 before the actual neutron interferometric experiment is explained. Particle , moving in -direction, is interacting with a time-dependent magnetic field with unit vector . The magnetic field rotates slowly with an angular velocity around the -axis under an angle , which is schematically illustrated below.
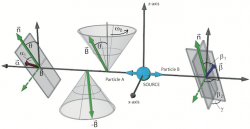
Now we considering an entangled state of two spin- particles, e.g., the antisymmetric Bell singlet state , where particle couples twice to the adiabatically rotating magnetic fields as described above. Consequently only one subspace of the Hilbert space is influenced by the phases acquired due to the interaction with the rotating magnetic fields. To identify the Berry phase the initial Bell singlet state is decomposed into the eigenstates of the interaction Hamiltonian , which yields . Next the dynamical effect which would dominate the geometrical one is eliminated, by using the so called phase-echo method. First the propagating particle is subjected to the rotating magnetic field in the direction for one period and therefore picks up a phases. Afterwards the particle passes another rotating field which points in direction again for one period, canceling the dynamical phase contributions. According to this phase-echo arrangement the state picks only a geometric phase which can be written as , where being a geometric phase. Next, a Bell-like inequality in CHSH-formalism (see here for details) is introduced, consisting of four expectation values with the associated directions , and , for joint measurements of spin for particle and , which results in
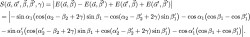
Without loss of generality one angle can be eliminated by setting, e.g., (). Keeping the polar angles , and constant at the usual Bell angles , , (and azimuthal parts fixed at ) is given by, where the familiar maximum value of is reached for . For the value of approaches zero.
Polar Angle Adjustment – Here the case is considered when the azimuthal angles are kept constant, e.g., . The polar Bell angles yielding a maximum -value, can be determined, with respect to the geometric phase , by calculating the partial derivatives (the extremum condition) of . The solutions are given by , and . With these angles the maximal decreases for and touches at even the limit of the CHSH inequality .
Azimuthal Angle Adjustment – Next the situation is discussed where the standard maximal value can be achieved by keeping the polar angles and constant at the Bell angles while the azimuthal parts, and , are varied. Here the maximum value is reached for and .
Geometric phase in a single-neutron interferometer experiment
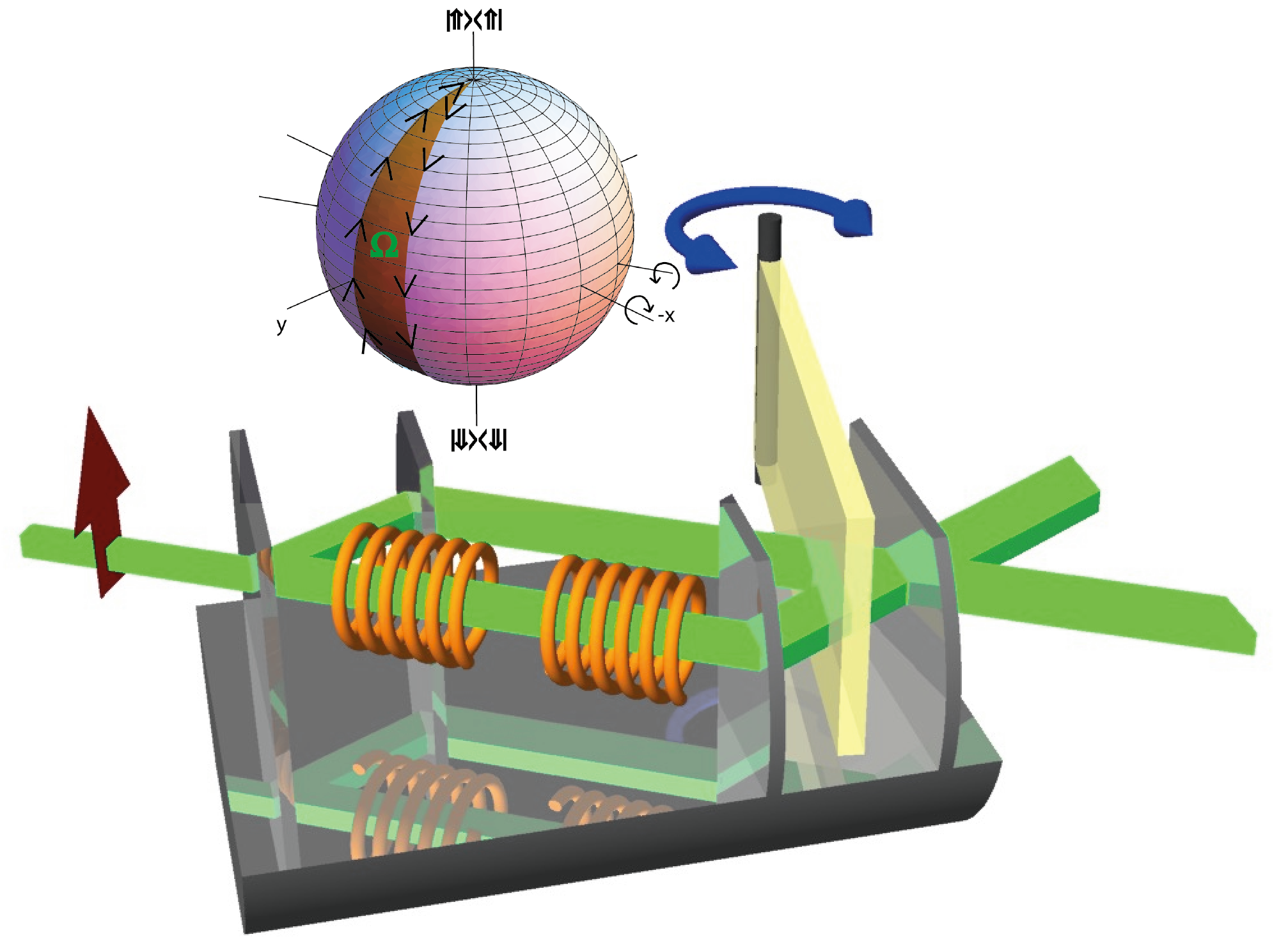
Following the notation from above, in our interferometer experiment 2 the neutron’s wavefunction is defined in a tensor product of two Hilbert spaces: One Hilbert space is spanned by two possible paths in the interferometer given by , and the other by spin-up and spin-down eigenstates, denoted as and , referred to a quantization axis along a static magnetic field. Interacting with a time dependent magnetic field, the spin-path entangled Bell-like state acquires a geometric phase tied to the evolution within the spin subspace. Interacting with a time dependent magnetic field, the spin-path entangled Bell-like state acquires a geometric phase tied to the evolution within the spin subspace . In contrast to the theoretical framework above, here only a geometric phase factor of is acquired, since only one sub beam is interacting with the magnetic field. Unlike in the proposed scheme for two entangled spin- particles, in the experimental realization, which is schematically illustrated below (left), a geometric phase of Aharonov and Anandan type, i.e. non-adiabatic and cyclic is accumulated, since the RF spin flip is a non-adiabatic process.
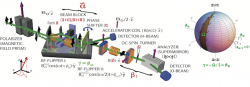
Manipulation of geometric and dynamical phases – The effect of the first RF-flipper, placed inside the interferometer (path I), is described by the unitary operator , which induces a spinor rotation from to , denoted as . The rotation axis encloses an angle with the -direction, and is determined by the oscillating magnetic field . Without loss of generality one can insert a unity operator, given by , yielding , where can be interpreted as a rotation from to , with the -direction being the rotation axis (), and describes a rotation about the same axis back to the initial state . This spin rotation is indicated by the “virtual” RF flipper in the interferometer setup depicted below (left). Consequently, can be identified to induce the geometric phase , along the reversed evolution path characterized by ( to ), followed by another path determined by ( to ). In the rotating frame of reference the two semi-great circles enclose an angle and the solid angle , yielding a pure geometric phase , which is illustrated above (right). The entangled state is represented by including the geometric phase and a time-dependent dynamic phase . In the next step an experimental strategy to cancel the dynamic phase component, by use of an additional (second) RF-flipper outside the interferometer 3 (more details here) and an additional Larmor precession within a tunable accelerator coil with a static field, pointing in the -direction is applied. The final results for polar (left), azimuthal (middle) and no adjustment are plotted below.

Our experiment demonstrates that a geometric phase in one subspace does not lead to a loss of entanglement, determined by a violation of a Bell- like inequality.
1. R. A. Bertlmann, K. Durstberger, Y. Hasegawa, and B. C. Hiesmayr, Phys. Rev. A 69, 032112 (2004); [quant-ph/0309089]. ↩
2. S. Sponar, J. Klepp, R. Loidl, S. Filipp, K. Durstberger-Rennhofer, R. A. Bertlmann, G. Badurek, H. Rauch, and Y. Hasegawa, Phys. Rev. A 81, 042113 (2010). ↩
3. S. Sponar, J. Klepp, R. Loidl, S. Filipp, G. Badurek, Y. Hasegawa, and H. Rauch,Phys. Rev. A 78, 061604R (2008);
[quant-ph/0803.3545]. ↩