Confined Contextuality in Neutron Interferometry
November 9, 2017 1:08 pmQuantum contextuality, based on the Bell–Kochen–Specker theorem (see here for details), is one of the most counterintuitive aspects of quantum mechanics. When trying to assign predefined values at least one observable in a set of possible measurements fails to behave classically, but never but it is unknown which observable(s) specifically. If one takes a set of observables together with particular choices of pre- and post-selection, it is possible to localize the contextuality to specific observables. Following an important result from Pusey 2, any projector with a weak value below 0 or above 1 is a proof of contextuality – using a generalized definition of contextuality proposed by Spekkens 3 (see here for Spekkens generalized definition of contextually).
Our experiment considers independent neutron spins (up to 17 qubits), which are prepared (pre-selected) in the product state and post-select onto the product state . Since the predictions of products of and by a non-contextual hidden variable theory (NCHVT) must be consistent with these boundary conditions, only products involving are left undetermined, e.g., products of projectors . By weakly measuring (see here for theory of weak measurements) such products, we reveal where value assignments from any NCHVT are inconsistent with quantum mechanics.
The link between contextuality and weak values follows the Aharonov–Bergmann–Lebowitz (ABL) formula 4, which gives the probability of obtaining a particular strong measurement outcome , between a preparation and a postselection , where the outcome corresponds to a projection operator . An ABL probability of 1 must be reproduced in any NCHVT. The ABL formula can be expressed in terms of weak values as with , being weak value the of the projectors in the intermediate measurement basis such that . From that and follows that implies . Furthermore, if contains only two outcomes (dichotomic operator), then it also follows that implies . In this case, measuring a weak value of 1 implies that any NCHVT must also assign a value of 1 (and a value of zero to all orthogonal projectors).
3 qubit case – pairwise correlations:
Each row or column (measurement context) of the square, illustrated below, mutually commutes. The very left square indicates that, according to quantum mechanics, the product of the three 3-spin measurement outcomes in each row is +1 (thin line), while their product in each column is −1 (thick line). A particular preparation and postselection fixes the values of two rows, as seen in the middle plot. In any noncontextual hidden variable theory, the remaining values must be −1, which is explained in the next paragraph in detail. This confines the BKS contradiction to the top row indicated by the red line, thereby localizing contexuality. This also demonstrates the quantum pigeonhole paradox 5 (see here for experimental details and theory): all pairs in the row appear anticorrelated, which violates the classical pigeonhole principle. Weak measurements confirm the paradox, revealing the correlation of each pair to be −0.972 ± 0.132, −1.050 ± 0.140, and −1.020 ± 0.137, from left to right.
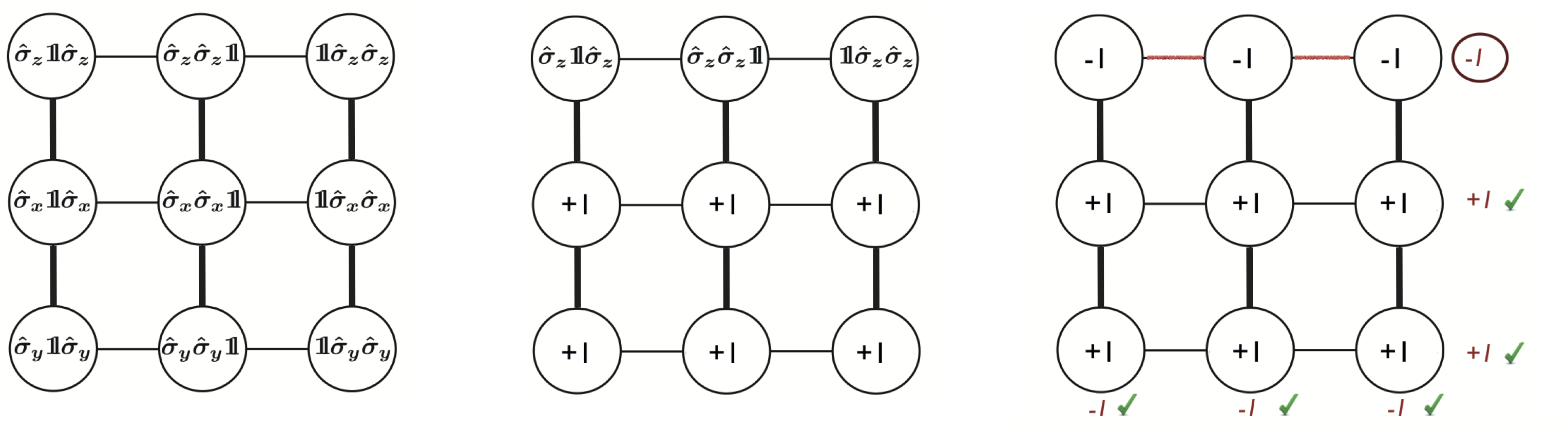
For our specific case of N = 3 we consider a product operator for any two spins out of the three spins, has a spectral decomposition as , where , which accounts for projections onto the same state (and therefore for correlation of the two spins and ) and for projections onto different states (anti-correlation). A simple calculation reveals and . Applying the Aharonov–Bergmann–Lebowitz (ABL) formula 4, expressed in terms of weak values as with , we get and and finally yields , as illustrated in figure above. Thus the projector is a so-called forbidden assignment for pairwise correlations.
3 qubit case – full correlations:
In a next step we investigate the projectors corresponding to such forbidden assignments for N = 3. Such a complete sets of forbidden projectors like this will be referred to as contextual bases, expressed as
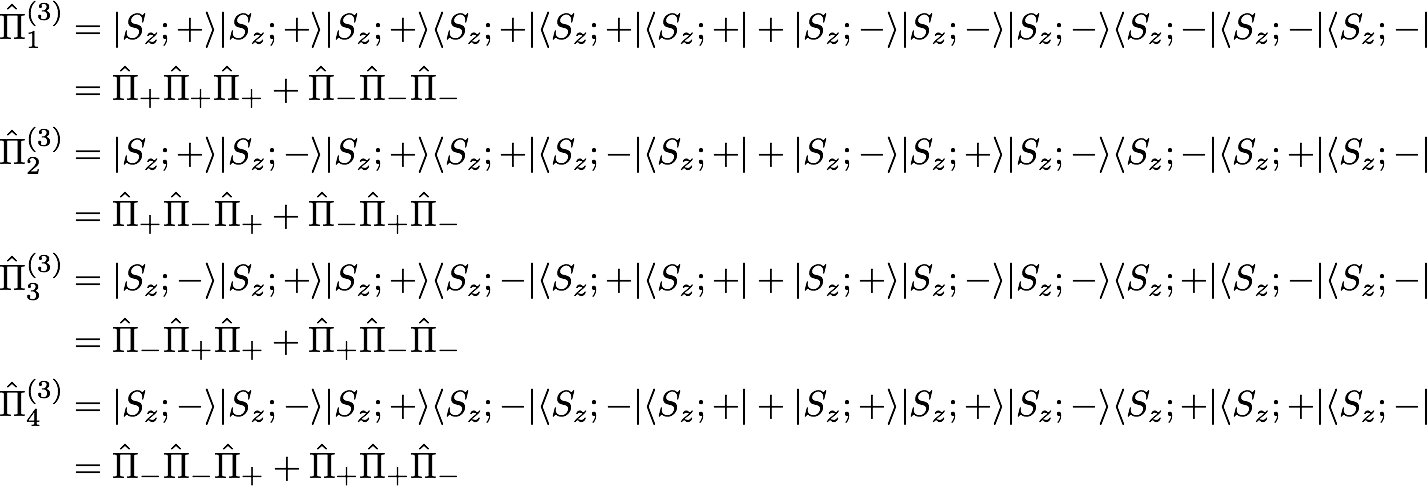
As already stated, following an important result from Pusey 2, any projector with a weak value below 0 or above 1 is a proof of contextuality – using a generalized definition of contextuality proposed by Spekkens 3. We find projectors with anomalous weak values in the contextual basis from above, constituting the first direct observation of localized BKS contextuality. As an explicit example, the weak value of , given and simplifies to , where each is a distinct spin, and is a single-spin weak value.
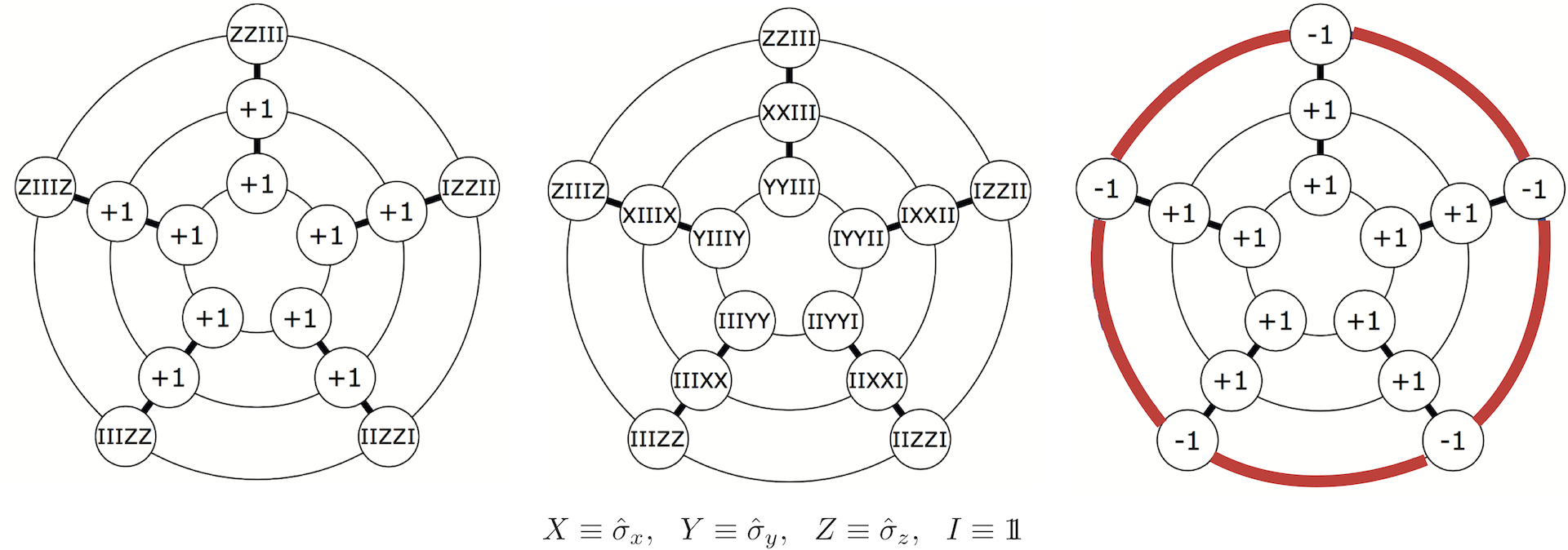
5 qubit case – full correlations:
Now we consider the N = 5 scenario, where analogously to the square ( N = 3) the contextuality is confined to a context in the 5 -spin Wheel-set consisting of 5 pairwise observables arranged in a ring – again all pairs as before (since ). (left) The product of the five observables in each ring is (thin line), and the product of the observables in each spoke is (thick line). (middle) A particular preparation and posts- election fixes the values of two rings. (right) In any non-contextual hidden variable theory, the remaining values must be −1, which confines the BKS contradiction to the outer ring, indicated by a red circle.
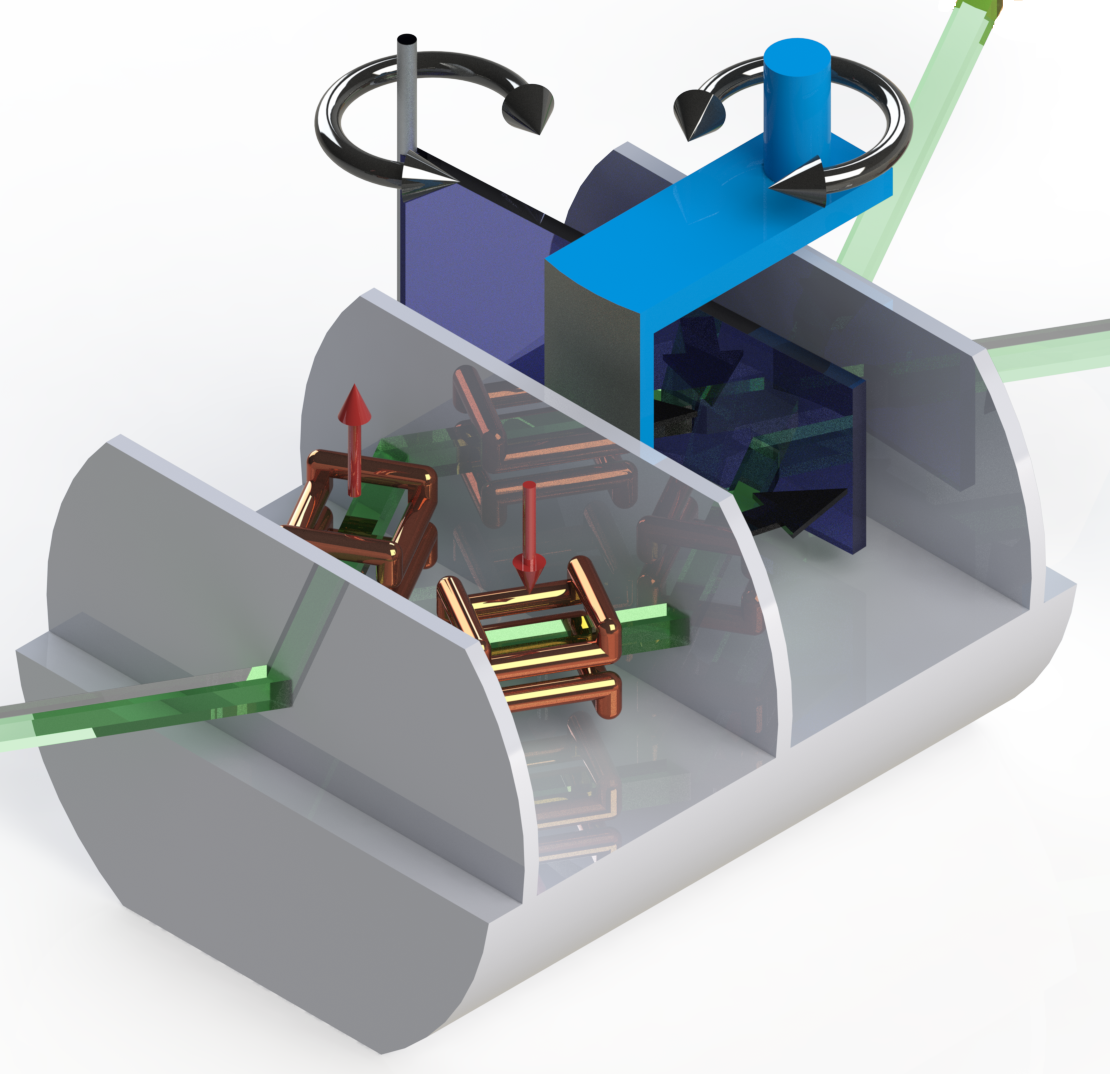
Experimental setup:
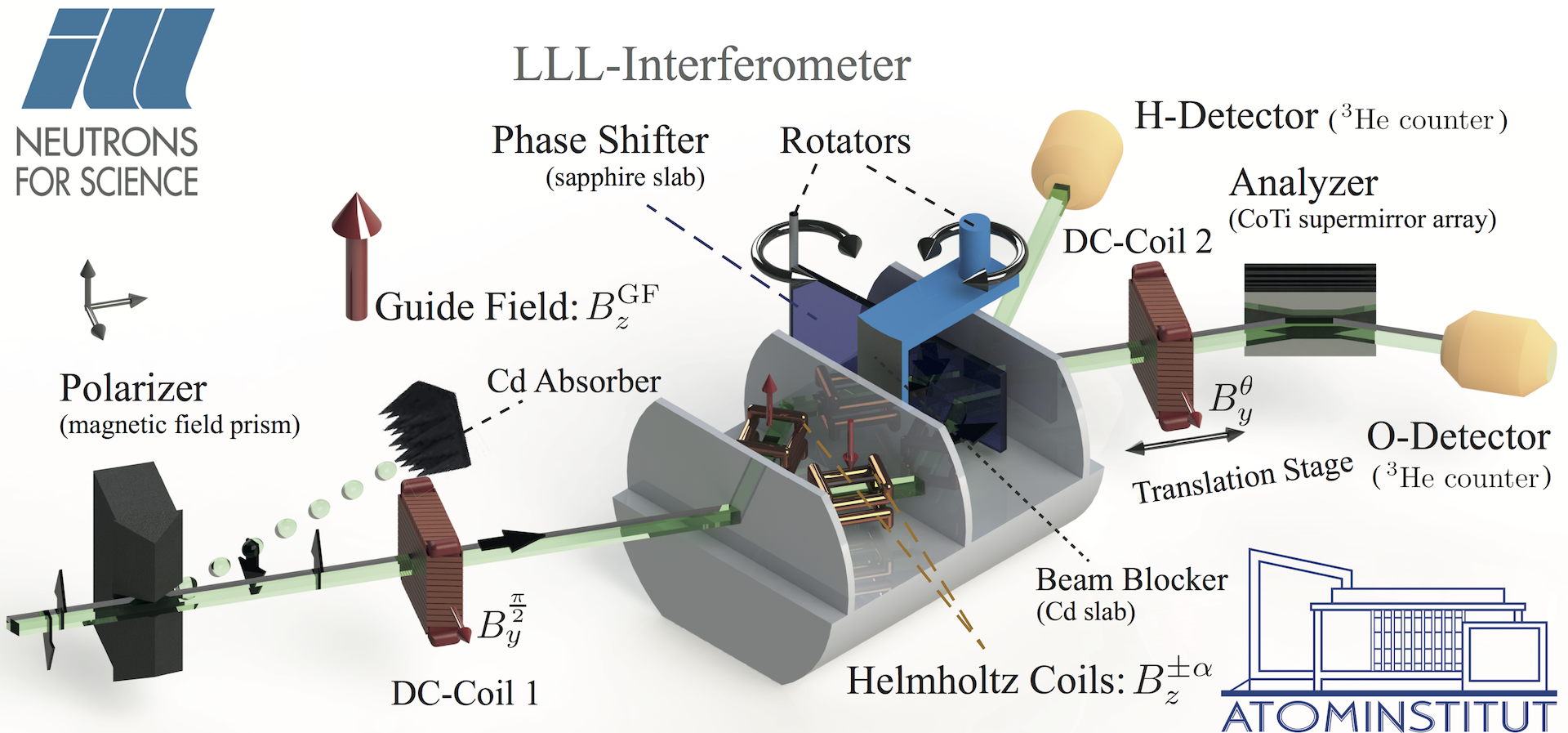
A schematically illustration of the setup is given below. A monochromatic neutron beam with a wavelength of Å is polarized by magnetically birefringent prisms. A DC coil placed in front of the interferometer preselects the neutron spin into the state . At the interferometer’s first plate, the beam is split into two paths by amplitude division. In each beam path a small coil in Helmholtz configuration generates magnetic fields in the direction and the neutron spin precesses in the -plane around these fields. These path dependent spin rotations lead to an entanglement between the spin and path DOF. In our experiment the fields were tuned so that the they caused a strictly positive rotation in path I and a strictly negative one in path II around the -axis. For all measurements the angle of rotation was set to . A phase shifter in combination with a Cadmium beam block mounted on a rotational stage offers full control over the neutron’s path DOF for the pointer readout. The phase shifter makes it possible to change the path qubit state in the equatorial plane, while the beam block can be used to access the path eigenstates at the poles. Of the two outgoing beams of the interferometer only the O-beam (forward direction) is spin analyzed. The second DC coil mounted on a translation stage in combination with a polarizing supermirror is used to postselect the final spin state . A detailed description of the experimental procedure to determine can be found here.
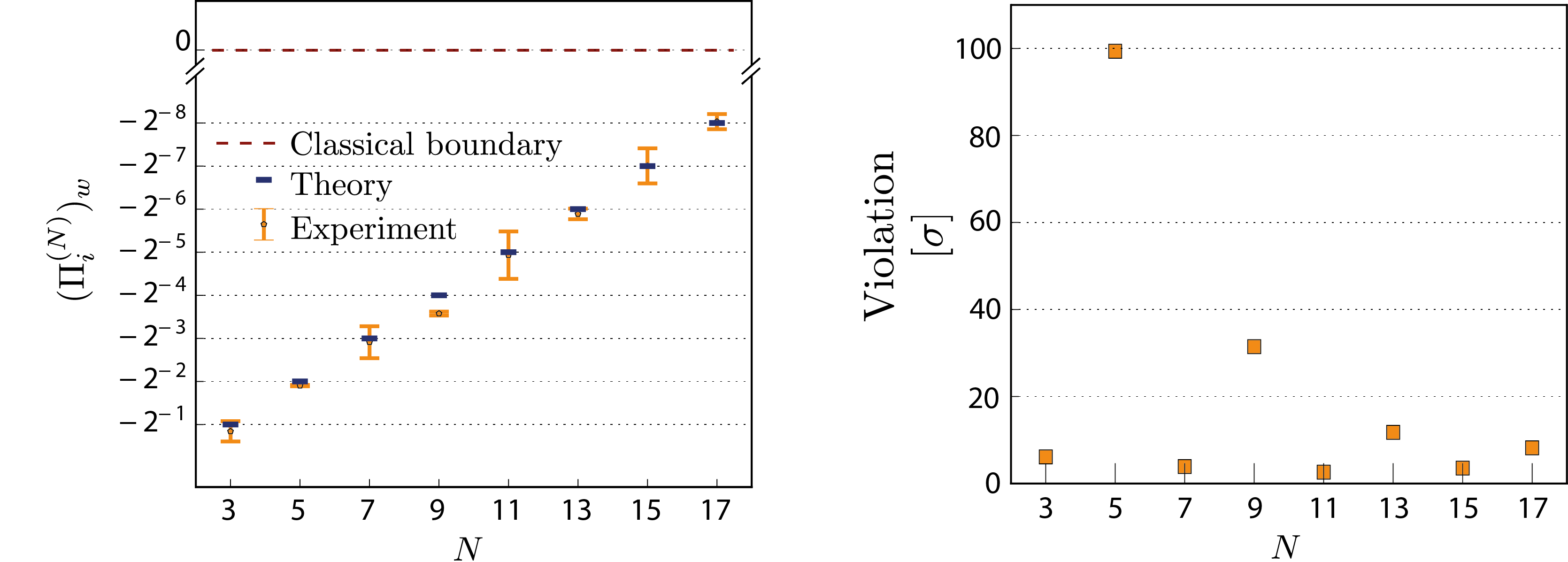
N qubit case – final results:
The weak values of the forbidden projectors (witness observables) in this contextual basis are expressed as , where where is the digit of , being the -digit binary sequences , , for example and . In the plot below our final results 6 for the contextually observable are depicted from N = 3 to N = 17 (error bars represent one standard deviation). The ideal analytic values are are plotted in blue. In right panel the number of standard deviations by which the measured weak value violates the classical bound of 0 is given.
It is worth noting, that, unlike existing approaches to demonstrating BKS-contextuality, our witness does not require entangled preparations or measurements, or indeed any interaction between the different spins at all. In our experiment we make use of N independent neutron spins.
1. S. Kochen & E. Specker, J. Math. Mech. 17, 59 (1967).↩
2. M. F. Pusey, Phys. Rev. Lett. 113, 200401 (2014).↩
3. R. W. Speakers, Phys. Rev. A. 71, 052108 (2005).↩
4. Y. Aharonov, P. G. Bergmann, and J. L. Lebowitz, Phys. Rev. 134, B1410 (1964).↩
5. Y. Aharonov, F. Colombo, S. Popescuc, I Sabadini, D. C. Struppa, and J. Tollaksen, Proc. Natl. Acad. Sci. USA 113, 532 (2016).↩
6. M. Waegell, T. Denkmayr, H. Geppert, D. Ebner, T. Jenke, Y. Hasegawa, S. Sponar, J. Dressel, J. Tollaksen, Physical Review A 96, 052131 (2017) ↩