Violation of the classical Pigeonhole Principle in Neutron Optics

The pigeonhole principle, first stated by Dirichlet in 1834 and therefore also reffered to as Dirichlet’s box principle or Dirichlet‘s drawer principle (“Schubfachprinzip”), states the following: “If you put three pigeons in two pigeonholes, at least two of the pigeons end up in the same hole.” In our neutron interferometric experiment ¹ the role of the two holes or boxes  is replaced by the two spin eigenstates and . Using our neutron optical approach for weak measurements of the Pauli spin operator (see here for details) allows for an experimental violation of the classical pigeonhole principle  – demonstrating the quantum pigeonhole effect ². Our pre-selected (initial) product state of the three neutron spins is given by , with  and the post-selected (final) product state of spins is , with (see here for details of the theory). A product operator for any two spins of the three spins, has a spectral decomposition as , where , which accounts for projections onto the same state  (and therefore for correlation of the two spins and ) and for projections onto different states (anti-correlation). A simple calculation reveals and . Applying the Aharonov–Bergmann–Lebowitz (ABL) formula ³, which gives the probability of obtaining a particular strong measurement outcome , between a preparation and a postselection , where the outcome corresponds to a projection operator . The ABL formula can be expressed in terms of weak values as with , which gives and and finally yields . This pairwise constraint is the quantum pigeonhole effect, with the spin eigenstates correspond to two boxes in which pigeons may be placed – the pigeonhole principle states that if pigeons are placed in two boxes, then at least one box must contain multiple pigeons. However, the constraint for all pairs implies that, regardless of how many pigeons are placed in the two boxes, no two pigeons are ever in the same box!

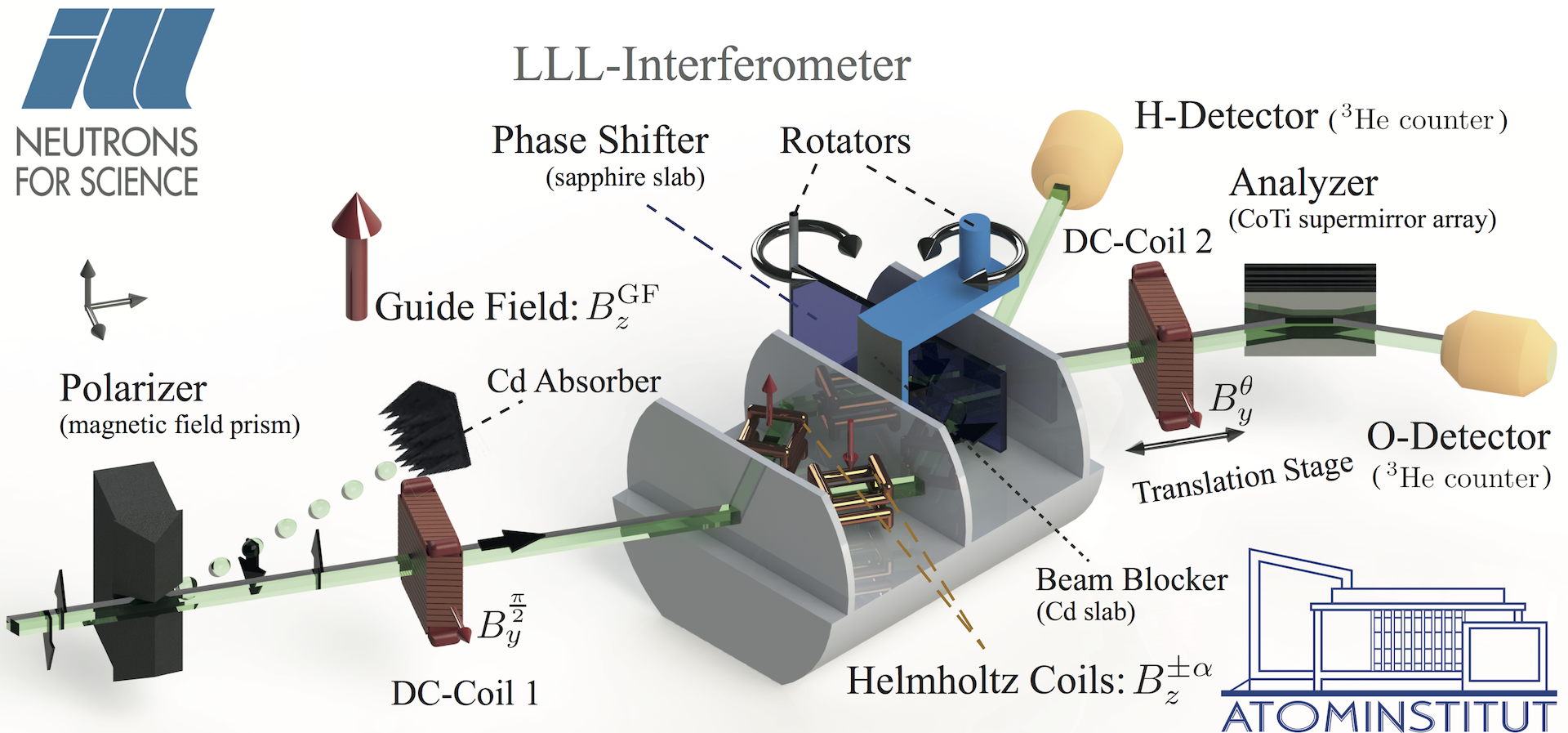
The experiment was carried out at the neutron interferometer instrument S18 at the high-flux reactor of the Institute Laue-Langevin (ILL) in Grenoble, France, a schematical illustration is depicted above. In our setup we measure the weak value of the neutron spin in the -direction applying an interferometer. The neutron’s path is used as a pointer to measure both the real and imaginary parts of , which has already been successfully used to completely determine weak values of massive systems ⁴. In our setup two magnetically birefringent prisms (Polarizer) split the unpolarized beam in two sub-beams, one with the neutron spin aligned parallel to the positive z-direction and one aligned antiparallel. Even though the angular separation is just four seconds of arc (exaggerated in illustration), only the beam with spin up component fulfills Bragg’s condition at the interferometer’s first plate. The other spin-down sub-beam passes through the first plate of the interferometer unaffected and does not further contribute to the experiment since it is absorbed by a small Cadmium slab. next the coil DC-Coil 1 rotates the initial spin form to due to Larmor precession within the coils’s magnetic field pionting in -direction in inducing a spin-rotation, therby completing the spin preselection, preparating the state . At the first interferometer plate, the beam is coherently split by amplitude division. In each path a spin rotator coil (in a Helmholtz configuration) produces a weak magnetic field in the – direction, causing (weak) entanglement between the spin and path degrees of freedom of each neutron. Between the second and final interferometer plate, a sapphire phase shifter is inserted, which in combination with a Cadmium beam block mounted on a rotational stage provides full control over the neutron’s path for the pointer readout (phase shifter changees the path state in the equatorial plane of the Bloch sphere, while the beam block permits access to the path eigenstates at the poles). At the third interferometer plate, the two paths are recombined and DC coil 2, in combination with a CoTi supermirror array allows for post-selection of the spin state . Finally the neutrons are detected by He counter tubes.

The measured values of are used to construct the pairwise anti-correlations . In general the weak value of a product of operators is not equal to the product of weak values of the operators. However, if initial and final states are given by product states, as it the the case ion our experiment holds. In addition, according to the ABL rule, we have . Our final experimental results are plotted above. All  pairs violate the classical pigeonhole principle, which is clearly illustrated by our experiment, demonstrating the quantum pigeonhole effect.

1. M. Waegell, T. Denkmayr, H. Geppert, D. Ebner, T. Jenke, Y. Hasegawa, S. Sponar, J. Dressel, J. Tollaksen, Physical Review A 96, 052131 (2017) ↩

2. Y. Aharonov, F. Colombo, S. Popescuc, I Sabadini, D. C. Struppa, and J. Tollaksen, Proc. Natl. Acad. Sci. USA 113, 532 (2016). ↩

3. Y. Aharonov, P. G. Bergmann, and J. L. Lebowitz, Phys. Rev. 134, B1410 (1964). ↩

4. S. Sponar, T. Denkmayr, H. Geppert, H. Lemmel, A. Matzkin, J. Tollaksen, and Y. Hasegawa, Phys. Rev. A 92, 062121 (2015).
 ↩