Weak Spin-1/2 Measurements
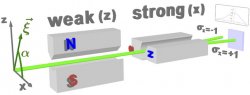
February 25, 2013 4:02 pmThe original experiment proposed by Yakir Aharonov, David Z. Albert and Lev Vaidman (AAV) 1 involves a beam of massive spin- particles. The observed quantum system is represented by the spin of a particle, while the probe system is formed by the particle’s spatial wave function. A schematic illustration of the measurement apparatus from the AAV gedanken experiments is given below A beam of particles, initially polarized in -direction, where is chosen to lie in the -plane with an angle in respect to the -axis. The prepared (or initial) beam, pre-selected with spin pointing in direction , passes through a weak magnetic field gradient, with the field pointing pointing in -direction. Here “weakly” means that the beams are still overlapping, hence one cannot get complete information of the spin direction (in a strong measurement they would be clearly separated). The weak interaction causes a coupling of the spin with the two slightly shifted partial spatial wave functions correlated to the two values of . Next the beam passes another Stern-Gerlach apparatus, splitting it into two spatially separated sub-beams corresponding to . The weak value of is determined from the post-selected spin component, via the deflection of the spot on the screen in -direction. The -distribution of the spatial wave function is detected via counts observed on the distant screen and directly reflects the distribution of ‘s (momentum distribution) in the final beam.
Our experiment 2 makes use of a beam of neutrons — massive spin- particles — as originally proposed by AAV 1. A direct implementation of the setup from depicted above is not a trivial issue due to the fact that the coherence length of the matter-wave beam is of the same order, or even less, than the resolution of available position sensitive detectors. This circumstances call for a different approach. The idea is to couple the spin that shall be measured weakly to another two-level system as a probe system rather than using a probe system which is gaussian distributed in the canonical variables. Our two-level probe system (measurement device) is formed by the two paths of a neutron interferometer, denoted as path I and II, to which the -component of the neutron’s spin is weakly coupled, which is schematically illustrated below. Details of the underlying theoretical work of our experiment can be found here. The experiment was carried out at the neutron interferometer instrument S18 at the high-flux reactor of the Institute Laue-Langevin (ILL) in Grenoble, France.
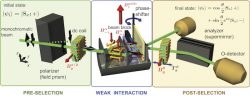
The experiment consists of three steps:
(i) Pre-selection: A monochromatic beam crosses a birefringent magnetic prism, which produces a field in -direction. Due to the spin-dependent birefringence (a few seconds of arc between the parallel and anti-parallel spin state), only the spin-up component fulfils the Bragg condition at the first interferometer plate (beam splitter), resulting in an initial polarization in -direction. Next the beam enters a static magnetic guide field (also pointing in the -direction), which covers the entire setup and prevents depolarization. Before the neutron beam enters the interferometer, the neutron’s spin is rotated into the -direction by a spin-turner. Inside this coil the spin precesses about the -axis, due to Larmor precession, thereby preparing the initial spin state denoted as .
(ii) Weak interaction: Small spin rotations are introduced by local modification of the static guide field. As a result, the Larmor frequency is increased in path I and decreased in path II, leading to the different spin rotations of . The coupling of spin and path DOF is expressed by the interaction Hamiltonian , where is the neutron’s magnetic moment and and are projection operators to paths I and II. Before the two sub-beams are recombined at the third plate, an adjustable relative phase factor is induced by a phase shifter plate. The phase shift is given by with atom density in the phase shifter plate of thickness , the coherent scattering length and the neutron wavelength .
(iii) Post-selection: The spin is rotated by a polar angle inside a dc spin turner coil, which is mounted on a translation stage. The polar angle can be set by adjusting the coil’s static magnetic field . Depending on the position of the translation stage, the azimuthal angle is tuned due to Larmor precession in the static magnetic guide field. The spin is finally selected by a spin-dependent reflection from a bent Co-Ti supermirror array. These apparatus make it possible to post-select an arbitrary final spin state . The outgoing beam is measured using a He-detector, with an efficiency over 99 %, from which real and imaginary part, as well as the absolute value of the -component of the neutron’s spin is determined. Ignoring terms of higher, which is exactly the approximation from the AAV 1 paper, real part modulus of the weak value of of are given by and . The imaginary part of of the weak value of of is given by . The final results are plotted below, for various finial spin states :
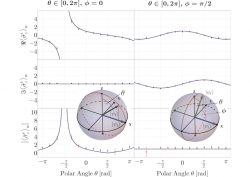
Experimentally determined real (top panel), imaginary component (central panel) and modulus (bottom panel), of the weak value of the -component of the neutron’s spin, plotted together with the theoretical predictions (blue line). Bloch-sphere representations are given for pre- and post-selected spin state (left) and (right).
1. Yakir Aharonov, David Z. Albert, and Lev Vaidman, Phys. Rev. Lett. 60, 1351–1354 (1988). ↩
2. S. Sponar, T. Denkmayr, H. Geppert, H. Lemmel, A. Matzkin, J. Tollaksen, and Y. Hasegawa, Phys. Rev. A 92, 062121 (2015)
[quant-ph/1404.2125]. ↩