Larmor Precession

The temporal variation of an operator ’s expectation value, is given by , where the dot denotes quantities derived with respect to time. The derivatives of and are given by the Schrödinger equation: , which gives and . This yields , which can be written as , resulting in the Heisenberg equation, which describes the time dependent evolution of an operator’s expectation value. It tells us that temporal changes in an operator’s expectation value result from an explicit time dependence of the operator or its commutators with the constituents of the Hamilton operator of total energy. In reverse, the Heisenberg equation states that for a conserved quantity, denoted as , the corresponding operator must commute with the Hamiltonian : , from which immediately follows .

In a next step the Heisenberg equation shall be applied to the the Pauli Spin operator from the Pauli equation, i.e., the Schrödinger equation for spin magnetic interaction , which consists of the neutron kinetic energy and the Zeeman magnetic energy given by . The equation of motion of the expectation value of the Pauli Spin operator hence is given by , with the commutator calculated as

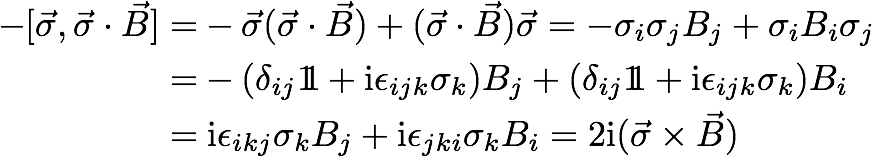
which gives , with being the gyromagnetic ratio. For a homogeneous magnetic fields (no spatial dependency) we have and using the definition of the polarization vector , we finally obtain , which is the motion of the vector of polarization in an homogeneous external magnetic field , which is referred to as Larmor precession.

R. Buchelt, PhD thesis “Spin Dynamics in Polarized Neutron Interferometry” (2000)