Radio Frequency (RF) flippers
March 29, 2017 10:10 amContents:
Semi-classical approach in rotating and oscillating field
Coupling to quantized oscillating field
Semi-classical approach
For a combination of a rotating radio-frequency (RF), with a frequency , and a static magnetic field, in a configuration known from nuclear magnetic resonance (NMR), the magnetic field is denoted as . The Pauli–Schrödinger equation for the neutron’s wavefunction is given by , which is solved with a separation ansatz denoted as , where denotes the neutron’s spatial wave function and the (time dependent) spinor wave function in matrix notation. This yields . Both sides must be equal to a constant given by , since the left side is only time depending and the right side only space dependent. The right side (only depending on the coordinate ), given by , and its solution is a plane wave given by , with .
However the spinor part remains much more complicated 1, where the equation , can be transformed with the substitution to . Now and are defined as and , which leads to . Next a unitary transformation is introduced, which transforms the equation in a system rotating around the -axis with a frequency of the magnetic field , yielding
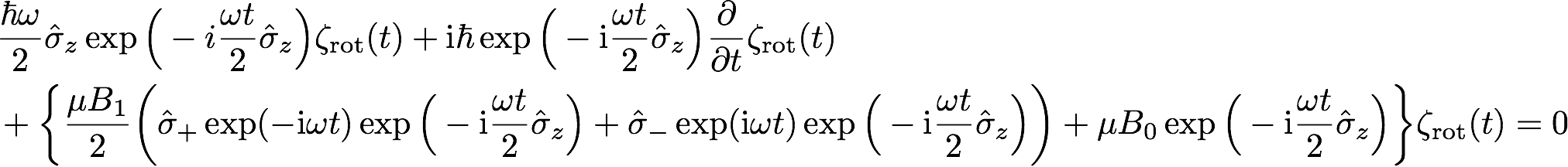
When the equation is multiplied with from the left side and the exponential function is expanded in a power series (with ) as , and using (with ) we get
![]()
and in the same manner . This leads to the following simpler equation:
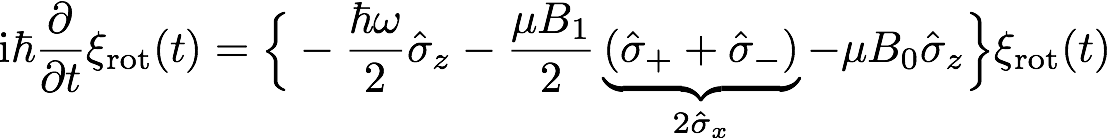
where the time dependency between the curly brackets has vanished. Now the following quantities are defined: and , which gives , where is the frequency of the rotating magnetic field, is related to the guide field and to the amplitude of the rotating field , as introduced above. Integration leads to the following equation:
. Since we get and in the non rotating system a solution is calculated as . Using the definition yields the final solution denoted as , with for instance accounting for an initial polarization pointing in -direction.
So far so good – the problem has been solved theoretically ! However what remains is to discuss the result and to understand its physical meaning. For this purpose, the second exponential has to be examined more precisely , discussing the linear expressions sequentially, we obtain and since we get . All together we finally obtain , with the time-independent unit-vector calculated as , with . In the rotating system, the neutron perceives the effective magnetic field .
In summary, the total wave function of the neutron can be expressed as . Using , and assuming the incident beam to be polarized in the -direction, i.e., and applying the Pauli matrices , and the identity matrix we finally get
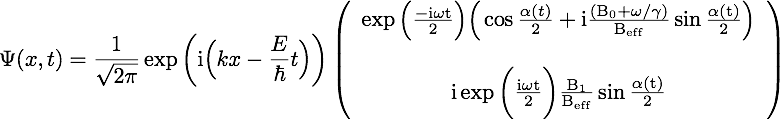
which for yields , that is a free particle of energy polarized in direction ( ).
If the rotating magnetic field has a resonance frequency , the action of the static field is completely compensated and has only a -component. This condition is referred to as frequency resonance. At this point we would like to consider the -component of the polarization given by which for frequency resonance reduces to . So if in addition the amplitude resonance for , namely , with being is the transmission time through the dynamical spin flipper with a flipper length , depending on the velocity of the neutron, is fulfilled we get ; a spin flip occurred ! If we now calculate the wave function after the spin flip we get
![]()
with , that is polarization in -direction. One can immediately see that compared to the total energy before the spin flipp, given by the neutron hast lost an amount of energy , by emission of a photon of frequency . In case of a flip from to the neutron absorbs an photon of the same energy from the rf-field.
However, in practice an oscillating field is used instead of a rotating one (though it is in principle feasible to implement a rotating filed). An oscillating field of frequency plus static magnetic guide field, denoted as , can be decomposed as the sum of two counter-rotating fields with frequencies :
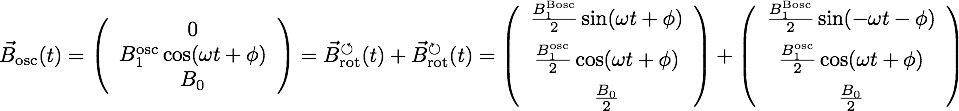
The interaction representation used above describes the physics in a rotating frame with the field component ω with the Larmor precession of the spin in the static field. The other component is seen in this frame as a fast rotating field (), whose effect can be neglected, which is referred to as rotating wave approximation (RWA). A consequence of the rotating wave approximation is the so called Bloch Siegert shift, which originates from the second term 2. In 1940 Bloch and Siegert proved that the dropped part, oscillating rapidly, can give rise to a shift in the true resonance frequency such that . Now the frequency resonance is given by and the amplitude becomes
The action of a resonance-frequency spin-rotator on the neutrons spin can be written using the unitary transformations , with the oscillation frequency of the resonance-frequency spin-rotator , and the polar angle of rotation . This is a rotation around -axes which is transformed into a frame rotating about the -axes at a frequency of . The phase of the resonance-frequency spin-rotator can be taken into account additionally, by an other unitary transformation .
Coupling to quantized oscillating field
The Hamiltonian of a the neutrons energy in an oscillating magnetic field, due to the neutrons magnetic moment, is denoted as , with . Next operators and are defined as and , having the following action on the spin eigenstates and . The quantized magnetic field for a single mode is given by , using the use of the creation and annihilation operators and . Using these definitions the Hamiltonian is given by
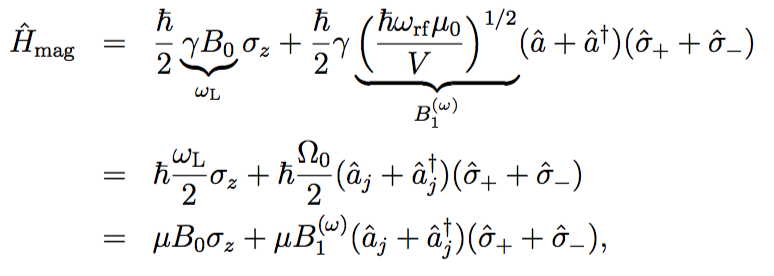
with the coupling strength . Hence, the total Hamiltonian consisting of the magnetic energy and the energy of the radiation field, is given by
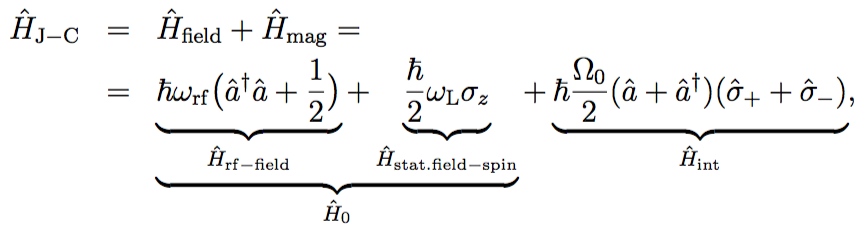
where the interaction Hamiltonian accounts for the coupling of the neutron with the radiation field, i.e. the energy exchange between the neutron and the quantized magnetic field. This Hamiltonian is referred to as Jaynes-Cummings (J-C) Hamiltonian 2, named after Edwin Thompson Jaynes and Fred Cummings.
The state vector of the oscillating field of frequency are represented by coherent states , which are eigenstates of and . The eigenvalues of coherent states are complex numbers, so one can write with . One can define a total dressed state 3 vector including not only the neutron system , but also the quantized oscillating magnetic field: , where for simplicity a single-plane-wave representation for the neutron’s wavefunction is chosen: At this point one can take a look at the action of the interaction Hamiltonian on a spin-up state 5:
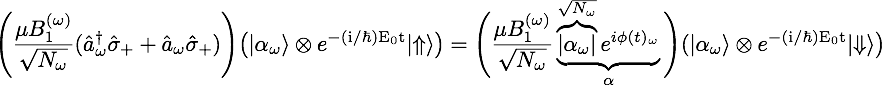
Here represents the usual coupling strength of the neutron field interaction which yields after the interaction with RF-field : a spin flip due to emission of a photon of energy and a phase factor from the coherent state of the oscillating field. Now the time evolution of a dressed state, as defined above, is taken into account .
As a last step we can rewrite this as , where is associated with a corresponding state vector , just like in an atomic two-level system, where a certain energy level is associated with a ground state . Hence can be identified with (in analogy to the exited state ). Thus our equation yields .
1. M. Suda, Quantum Interferometry in Phase Space, Springer (2006). ↩
2. F. Bloch and A. Siegert, Phys. Rev. 57, 522 (1940). ↩
3. E. T. Jaynes and F. W. Cummings, Proc. IEEE 51, 89 (1963). ↩
4. E. Muskat, D. Dubbers, and O. Schärpf, Phys. Rev. Lett. 58, 2047 (1987). ↩
5. S. Sponar, J. Klepp, R. Loidl, S. Filipp, G. Badurek, Y. Hasegawa, and H. Rauch, Phys. Rev. A 78, 061604R (2008); arXiv:quant-ph/0803.3545. ↩