Rotations in Hilbert Space

An arbitrary rotation in three-dimensional space can be described by three Euler rotations by angles , , about the , and -axis. Each rotation is thereby represented a rotation matrix . The sequential rotations are equivalent to a single rotation about an appropriate axis by an angle : , with . This orthogonal transformation rotates the physical system under consideration, while keeping the reference frame of , it is therefore an active rotation with respect to the system, expressed as . What is the transformation of the quantum-mechanical states that corresponds to the three-dimensional spatial rotation of the physical system performed in real space? A transformation that accounts for the vector property of a state vector in the two-dimensional Hilbert space of spin is required.

Let us first take a look at the different transformation behavior of scalars and vectors in three-dimensional space, where a rotation of a scalar field is transformed like  or . Upon transformation it features internal dependence on only, since  exists in space independently of any present system it is not transformed externally, it is not directed and therefore does not depend on the choice of the describing system. A vector field, on the other hand, very well depends in its representation on the system it is described by, hence it does not only transform internally, but with its components depending on the system, externally too, which is denoted as .

Now back to to the spinor rotations; a state vector in Hilbert space is rotated according to , where is defined in such way that it is equal to the vector of its eigenvalue transformed by the matrix in , namely . Hence, and . In order to conserve the norm of vectors in , must be unitary, which means and . We start with a wave function and asks for a representation of in terms of . Performing an infinitesimal rotation about to -direction (), we get for the coordinates of three-dimensional space

and consequently the wave function

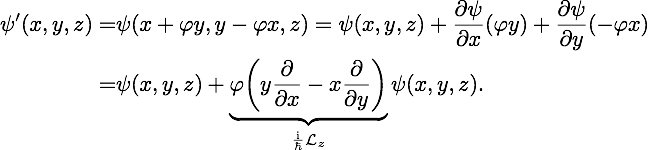
Here the bracket term corresponds to the functional representation of the z−component of the operator of orbital angular momentum  given by

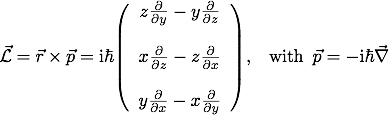
Therefore can be written as , or generalized with regard to an arbitrary orientation of a rotation axis , . This operator represents a differentially small rotation about . For a finite rotation, the above operator has to be applied (in the limit) infinitely often, which gives

because of

demonstrating that the operator is originator to the described rotation. Although the spin is independent of other degrees of freedom, it is an angular momentum and a vector operator that will likewise transform upon rotation of the system. With we finally obtain .

Because of , where we have again used , the sum can be split in a part with even and one with odd indices . Using , which leads to and , we finally get

It is instructive to take a look at the effect of the unitary operator on the spin eigenstate . We apply the operator , where is the rotation angle about the axes onto , which yields

This is the representation of an arbitrary (pure) spin state, represented by the two parameters , being the azimuthal and polar angle of the spin’s Bloch sphere representation, which is illustrated below.

R. Buchelt, PhD thesis “Spin Dynamics in Polarized Neutron Interferometry” (2000)