Greenberger–Horne–Zeilinger & W State Preparation

A Greenberger–Horne–Zeilinger (GHZ) state ¹ is a maximally entangled quantum state, which involves at least three subsystems. They are either represented by individual particles, as it is the case for photons, or degrees of freedom for single particle systems, like neutrons. GHZ states can be applied to prove the GHZ theorem as a way to disprove the concept of “elements of reality”, introduced by Einstein—Podolsky—Rosen in their attempt to prove that quantum theory is incomplete. The GHZ theorem is a significant improvement over Bell’s Theorem in a sense that it gives the opposite prediction — and not only a statistical violation like Bell’s Theorem — when compared with realistic theories (see here for details on the GHZ argument).

Experiments:

Preparation of Greenberger–Horne–Zeilinger (GHZ) states
Entangle witnesses for W-states

 Preparation of Greenberger–Horne–Zeilinger (GHZ) states

In our neutron interferometric experiment a newly developed method for coherent manipulations of the neutron’s total energy ² (see here for details) is applied allowing for successful preparation of a GHZ entanglement in the single neutron system ³. This is accomplished by exploiting the neutron’s interaction with an oscillating magnetic (RF) field, where photons are exchanged with the RF-field. The generated (triple) entanglement of the neutron’s spin, path and total energy degree of freedom,  can be expressed in terms of a state vector as

Interferometric setup for preparation of a GHZ-states

Measurement results of four expectation values were inserted in an equality, derived by Mermin, yielding a final value of , which is significantly larger than 2, the upper border of realistic theories. The expectation values are obtained by inducing relative phases between the orthogonal eigenstates of the individual quits, i.e., spin, path and total energy ⁴. Note that the energy subspace, in general, does not consist of only two discrete levels (that are addressed here) but has a continuous structure. Our results clearly contradicts the noncontextual (realistic) assumption and confirms the predictions of quantum mechanics as a contextual theory.

In so doing, we want to express that the use of entanglement of the energy degree of freedom is not limited to neutrons but is easily applicable to other quantum systems (atoms, ions a.s.o.). Furthermore, a coherent manipulation of the energy degree of freedom can be extended to create artificial multilevel quantum systems (e.g., of the order of ) in a single-particle system by applying a multiple-frequency energy-manipulation. In a neutron optical experiment without involving a spatial beam separation, where entanglement of spin, momentum and total energy degree of freedom is generated utilizing a suitable combination of radio-frequency and static magnetic fields ⁵.

 Entangle witnesses for W-states

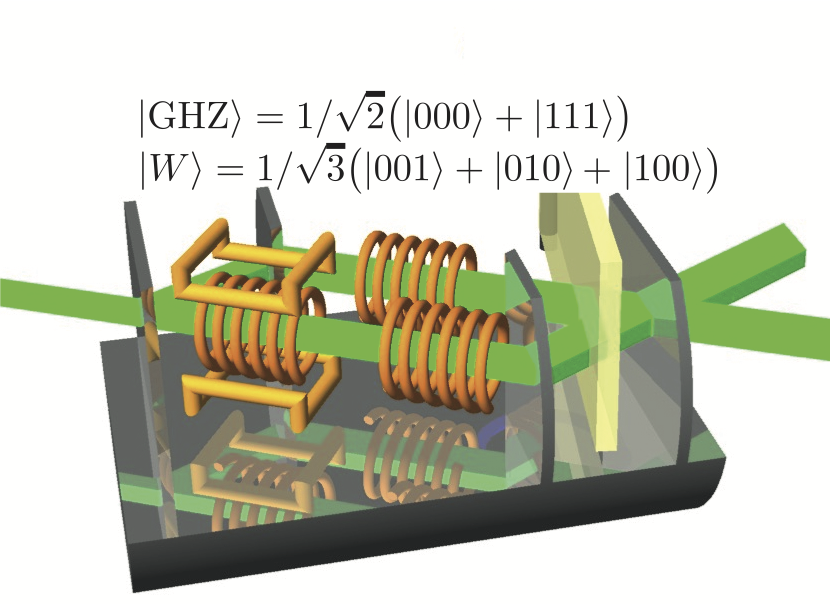
In a subsequent experiment ⁶ preparation of GHZ, as well as, W-states (see here for details) was our experimental target. The entanglement is detected via appropriately designed and optimized nonlinear witnesses. Via the applied criteria we reveal even finer properties of the type of the genuine multipartite entanglement that is produced in the experiment. The following sates were prepared using the setup depicted below:

Genuine tripartite entanglement of these states were analysed by proper nonlinear witnesses. A full tomography of the generated states would have been too complex and partly even infeasible (because certain coherences cannot be achieved). As entanglement witnesses do not require a full state tomography they clearly provide an advantage in this case. It is demonstrated that, only by measuring few matrix elements, different types of multipartite entanglement can be proven to be present in a single-neutron system. Our results show that quantum correlations can indeed manifest in different subsystems of a single physical entity.

Interferometric setup for preparation of a GHZ, as well as W-states.

Our revealed substructure of an entangled single-neutron system and high controllability opens the possibility for testing more fundamental and sophisticated properties of neutrons via exploring just this substructure.

1. D. M. Greenberger, M.A. Horne, A. Shimony and A. Zeilinger,  Am. J. Phys. 58, 1131 (1990). ↩

2. S. Sponar, J. Klepp, R. Loidl, S. Filipp, G. Badurek, Y. Hasegawa, and H. Rauch, Phys. Rev. A, 78, 061604R (2008); [quant-ph/0803.3545]. ↩

3. Y. Hasegawa, R. Loidl, G. Badurek, K. Durstberger, S. Sponar, and H. Rauch., Phys. Rev. A 81, 032121 (2010). ↩

4. S. Sponar, J. Klepp, G. Badurek, and Y. Hasegawa,., Phys. Lett. A 372, 3153-3156  (2008). ↩

5. S. Sponar, J. Klepp, K. Durstberger-Rennhofer, H. Geppert, M. Both, C. S. Schmitzer, H. Bartosik, G. Badurek, and Y. Hasegawa, New J. Phys. 14, 053032  (2013). ↩

6. D. Erdösi, M. Huber, B. C. Hiesmayr, and Y. Hasegawa, New J. Phys. 15, 023033  (2013). ↩