Generalized Eigenvalues – Weak Values obtained at arbitrary measurement strength

In the original framework of weak measurements, as developed by Yakir Aharonov, David Z. Albert and Lev Vaidman (AAV) ¹, the interaction between the measured quantum system and the coupling with the measurement device is supposed to be minimal disturbing. In 2010 Andrew N. Jordan and Justin Dressel proposed the concept of contextual values as a generalization of the eigenvalues of an observable that takes into account both the system observable and a general measurement procedure yielding statistics of post-selected measurements at arbitrary interaction strength ². However, the term has caused some confusion with the unrelated concept of contextuality as it applies to hidden variable models of the quantum theory. Therefore, we propose to call them as generalized eigenvalues of the observable . See here for a detailed theoretical treatment discussion generalized eigenvalues ³. Generalized eigenvalues are not the weak values themselves. Rather, the generalized eigenvalues are what you assign to each independent detector outcome, just like you would with eigenvalues for projective measurements contributing to the expectation (mean) values. The surprise is that conditioned averages of these generalized eigenvalues converge to weak values in the weak measurement limit. What our experiment shows is that conditioned averages of generalized eigenvalues can produce weak values in certain cases using any measurement strength. In a nutshell: generalized eigenvalues relate to weak values as eigenvalues relate to expectation values.

Considering a composite object-measureming device system, consisting of two qubit-systems. As in the case for minimal disturbing measurements the system’s preselected sate vector given by , which is illustrated below.

However, instead of performing a series expansion around the exact formula is used. The action of the evolution operator then gives

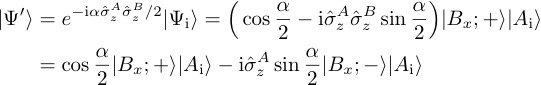
The postselection on the the final state then leads to

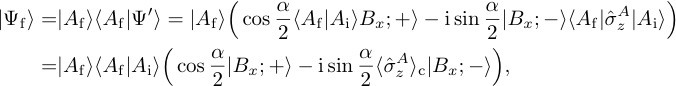
where denotes the contextual value of the Pauli operator , valid for all values of , i.e., for arbitrary measurement strengths. Again calculating the the six intensities  and yields

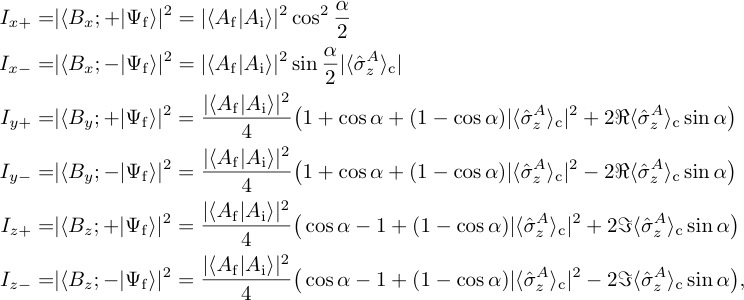
from which we later calculate the expressions of the weak value, being the real and imaginary part and the modulus of the weak value of the Pauli operator , holding for all values of .

In order to connect these expressions for the intensity from above with the generalized eigenvalue results introduced on the theory page, we focus on the real part of the weak value from above. Noting that this real part is obtained from the relative y intensities, we re-examine the structure of the y-intensity expressions. Recall that the initial spin state is , and the path-spin interaction can be written as . As such, if the y spin basis is measured, the path degree of freedom will be affected by the Kraus operators , such that the associated POVM elements are   (see here for an introduction towards POVMs). It is then obvious that assigning the values produces the operator identity  indicating that are the appropriate generalized eigenvalues to assign the spin pointer in the basis of y in order to measure . The conditioned average of generalized eigenvalues given the initial and final path states is using the intensities , equivalent to the intensities from above. The conditioned average then yields , which converges to the real part of the weak value in the limit , consistent with the general conclusions of the work from Dressel and Jordan ².

The experiment was carried out at our neutron interferometer instrument S18 at the high-flux reactor of the Institute Laue-Langevin (ILL) in Grenoble, France. A detailed schematically illustration of the interferometric setup is depicted below. The two quantum systems, denoted as system and  from the theory section, i.e, investigates system and pointer system, are represented in our experiment by the neutron’s path degree of freedom in the interferometer, our system that shall be investigated, and the spin of the neutron, our pointer system or measurement device.

Before the actual interferometric measurement procedure begins, the incoming monochromatic neutrons are spin polarized due to a spin-dependent refraction from a magnetic field prism. Next the initial state of our probe system (spin) is prepared by a rotation from to due to armor precession about the -axes within the  DC-Coil 1, in which the static magnetic field is adjusted in such way that it induces a spin rotation.  The actual measurement procedure then consist of three stages: i) Pre-Selection of the path state due to the first plate of the interferometer (50:50 beam splitter) and relative phase between the orthogonal path eigenstates. This is achieved by a parallel sided sapphire slab is inserted between the first and the second plate of the interferometer as a phase shifter. By rotating the phase shifter plate (with the thickness of the phase shifter plate , the neutron wavelength , the coherent scattering length and the particle density in the phase shifter plate) can be tuned systematically due to the different relative path lengths in path I and II. ii) Tunable interaction strength by utilizing coils in Helmholtz configuration in each beam path which allow for path-dependent spin rotations, coupling the neutron’s path and spin thereby. Two interaction strengths are chosen, namely deg for weak interactions and deg for strong interaction (orthogonal spin states). iii) Post-selection: At the third plate of the interferometer the sub-beams are recombined thereby caring out the path post-selection. Only neutrons traveling in the forward direction, i. e., with a relative phase , denoted as , are spin analyzed later, using a CoTi supermirror array. This procedure is called pointer read–out of the probe system, which in our case is represented by the neutron’s spin.  The spin analysis is performed by DC-coil 2 (see setup above), which is mounted on a translation stage, together with a CoTi supermirror. Inside the coil a tunable magnetic field is adjusted such that it rotates the spin by a polar angle . Thus, for spin analysis direction the polar angle is set to 0 and for we have . Depending on the coil’s position along the neutrons’ trajectory (translation stage), the spin’s azimuth angle  changes due to the spin’s Larmor precession within the magnetic guide field. Thus for spin analysis direction a polar angle in combination with azimuthal is set. Finally, for we get  together with . Subsequently the supermirror array (together with DC-coil 2) carries out a projective measurement along the direction defined by and . In a final step the neutrons are detected by the O-detector, a He counting tube.

Depicted above we have intensity modulations , with , of both measurement strengths, i.e., for weak and strong interaction. The six panels on the left hand side show interferograms of the weak interaction with deg. For both the pre- and post-selected spin state are , which results in a large count rate, in contrast to the count rate of which is is very low, since initial and final spin states are orthogonal. Next we have which are almost identical at half of the maximal possible count rate from before. Finally the interferograms are phase shifted by two times having as well half of the maximal count rate. In the six  panels the right hand side the interferograms for the strong interaction,  deg, are depicted. Resulting from the large spin rotation of in each beam path, now show the same average count rate, but are phase shifted by .  show almost no contrast in the case of strong measurements. The phase shift between and is now  deg and therefore easy to resolve compared to the weak interaction strength. Using the relations from the theory section (see here),  and  it is now possible to calculate real, as well as imaginary part and the modulus of   from the intensities given above, as

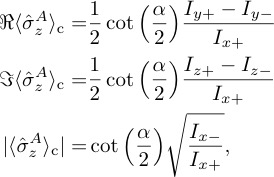
which is plotted below, both for weak interactions ( – left) and strong interactions ( – right).

In order to extract the real part of , , as well as , top panel in the above plot, the intensities and are required, where acts as a normalization factor. Since theory predicts the weak as well as the contextual values to be zero, and are very close. In addition, the interferograms of lose contrast for increasing , due to the fact that the spin rotation inside the interferometer approach orthogonality.

For the imaginary part of and the intensities and are required, where again acts as a normalization factor, while resolving the phase shift between and is crucial for determination of and . Since this phase shift is given by two times , it is obviously much harder to resolve in the weak interaction case, which is depicted above on the left, middle panel, compared to the contextual value with maximal interaction strength deg on the right side.

Finally the modulus of and , denoted as and , (bottom panels) are obtained using the intensities . The advantage of the strong interaction is intuitively understood: the discrimination of the relevant signal from the background is the crucial point, for degree is expected to be zero and the signal becomes larger with increasing make the discrimination easier.

Our measurement scheme is not limited to the neutron’s spin and path, but is in fact completely general and can be used for any coupling between two two-level quantum systems.

1. Yakir Aharonov, David Z. Albert, and Lev Vaidman, Phys. Rev. Lett. 60, 1351–1354 (1988). ↩

2. J. Dressel, S. Agarwal, and A. N. Jordan, Phys. Rev. Lett. 104, 240401 (2010). ↩

3. Tobias Denkmayr, Justin Dressel, Hermann Geppert-Kleinrath, Yuji Hasegawa, and Stephan Sponar, Physica B. 551, 339-346 (2018). ↩