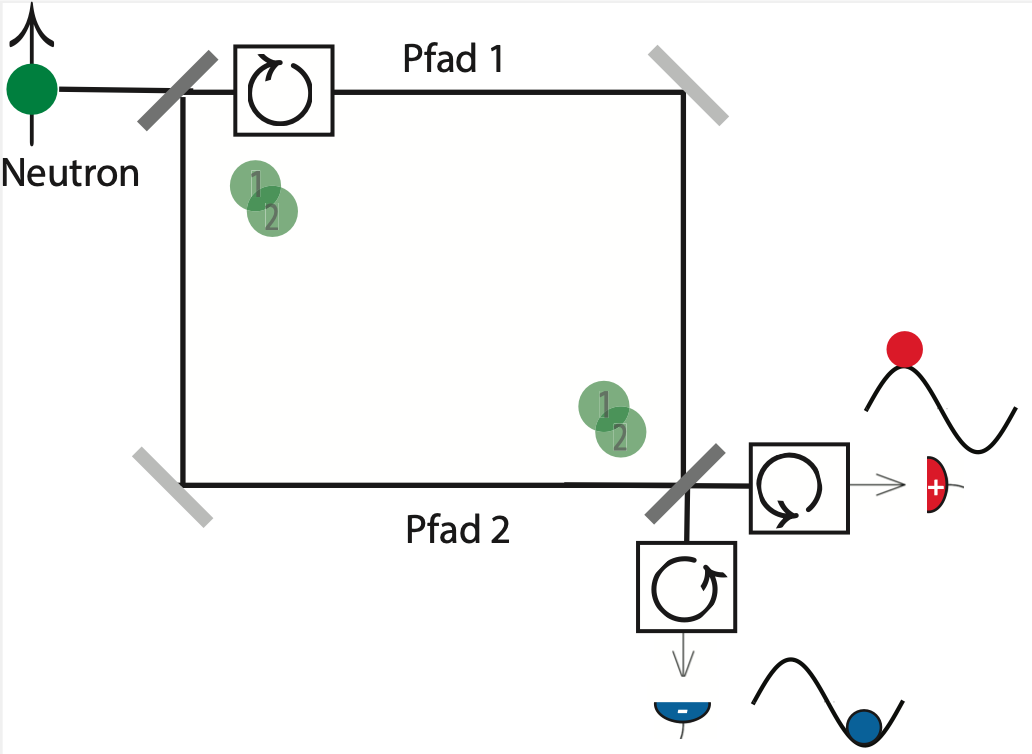
Quantifying the presence of a neutron in the paths of an interferometer
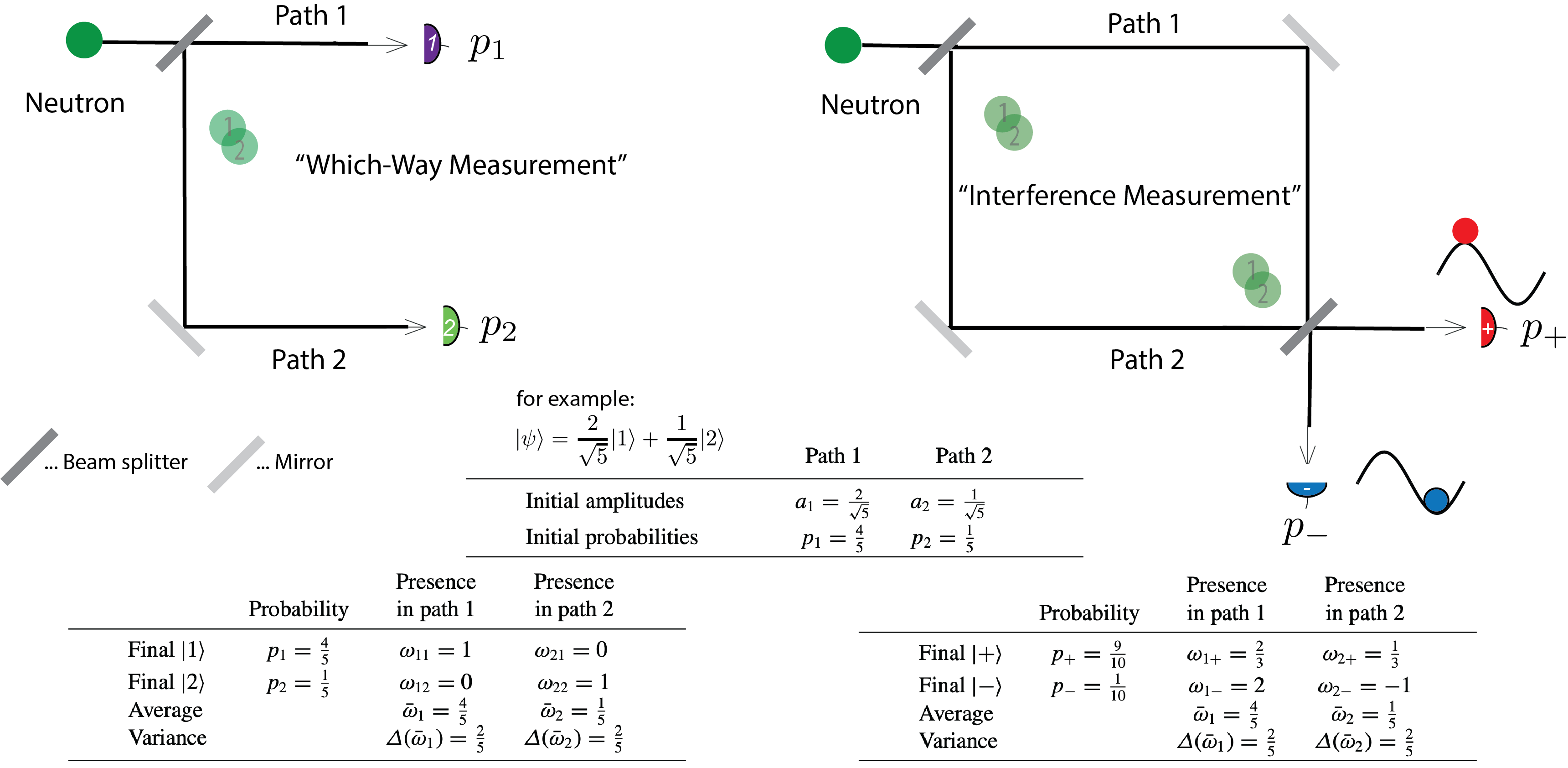
April 28, 2022 12:31 pmIt is commonly assumed that no accurate experimental information can be obtained on the path taken by a particle when quantum interference between the paths is observed. However, recent progress in the measurement and control of quantum systems may provide the missing information by circumventing the conventional uncertainty limits. This is achieved by introducing a quantity which we refer to as path presence 1. The path presence should not be confused with the amplitudes and of the initial state in an interferometer after the beam splitter (illustrated aside) given by , where and denote the eigenstates of path 1 and 2 respectively. The latter determine the detection probabilities in case a neutron detector is placed directly in one or the 
other path. This would be a naive which-way measurement which destroys the interference. In contrast, the path presence proposed here can be precisely measured while full interference is maintained; the two exit ports of the interferometer are described by the states and respectively, which also take the phase between the two paths into account as . The path presence always links an initial state to a final state. This means, one still cannot predict the path a neutron will take, but once the neutron has been detected in one or the other exit beam, one can in retrospect infer its presence in path 1 and 2 respectively. While we cannot predict the path, we are able calculate the statistical probability of detecting the neutron in path 1, which is given by the expectation value of the path projector . In the context of the which-way measurement (as illustrated below left) we measure in the eigenbasis of the operator, and obtain the expectation value by summing over the eigenvalues expressed as . Since an expectation value can be calculated by any complete basis, we chose the basis for the interference context, which is illutrated below on the right side. Now weak values, given by with final state , overtake the role of the eigenvalues. In this case now the expectation value is given by the averaged weak value . Hence, the detection probability can also be interpreted as an averaged weak value . Also the variance, accounting for the path uncertainty, can be calculated in either way. In the which-way context we get and in the interference context .
Feedback compensation 2: now a small spin rotation value , on the initial spin state , is induced in path 1. in the interference context the exit beams we compensate the rotation of the spin by rotating it back by an angle in the port and in the port (similarly in the which way context the corrections and are applied in path 1 and path 2, respectively). In general, different compensation angles in the two ports will be necessary for optimal compensation, indicating that the neutrons in the two exit ports have experienced different spin rotations in the interferometer, which is depicted below. Now we can evaluate the optimal feedback compensation effects for any interaction strength . However, larger values of reduce the visibility of interference fringes and make it more difficult to identify the universal features that characterize weak interactions. Here, we focus on the limit of a small interaction strength . Series expansions by show that the optimal compensations are to first order determined by the weak values as (see here for detailed calculation of the optical compensation and examples illustrating the concept of path presence). Simply speaking, in the limit of weak coupling, that means small values uf , the weak value of the path projection operator is given by the ratio of the spin rotation angle and the optimal compensation as – this ratio of angles is our new experimental accessible quantity, which we refer to as path presence.
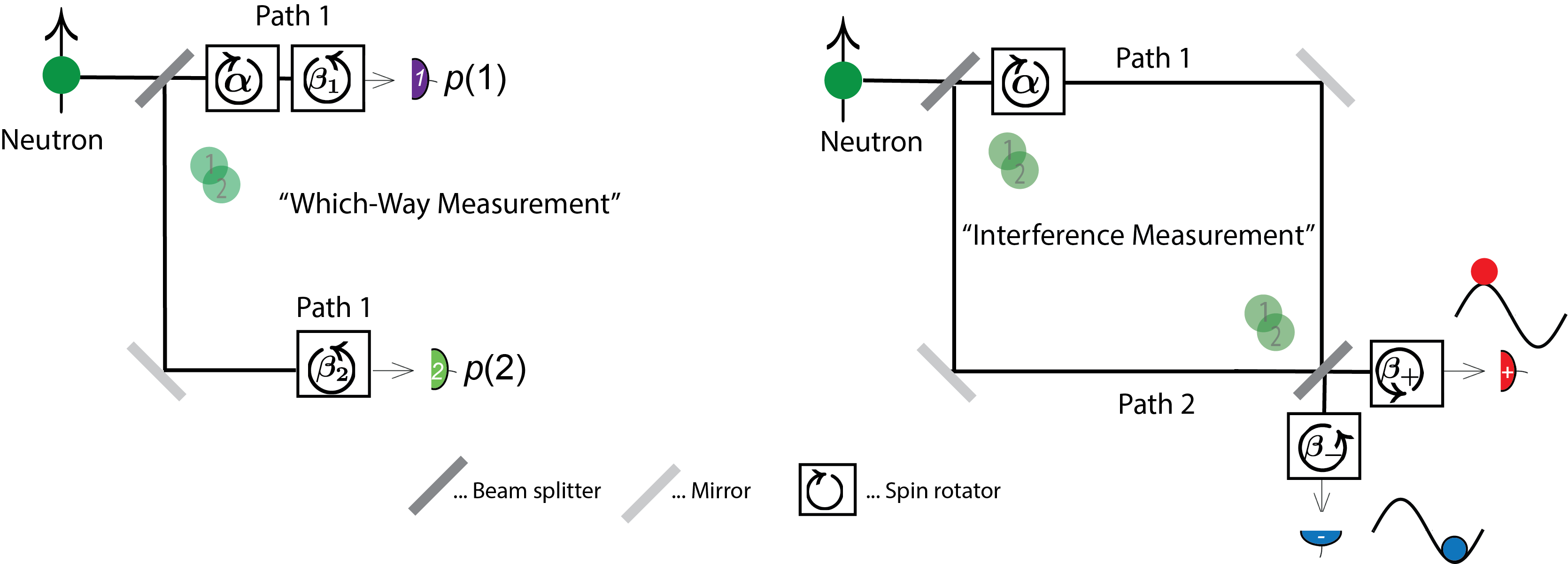
Unlike a usual weak measurement, in the feedback compensation scheme, we don’t measure individual spin components but determine the spin rotation relative to its initial state. This is done by applying the compensation, i.e. an estimated back rotation by , and measuring the spin in the original direction . The estimate is varied until reaches a maximum. In an ideal case and the variance of between events vanishes completely. Once the compensation is adjusted, every neutron verifies its correctness and the determined weak value can be attributed to every individual neutron.
Ozawa-Hall Error 3: the very same conclusion can be drawn using the Ozawa-Hall theory. Ozawa introduced a general concept of measurement errors (originally called noise) of an observable as . Here is the unitary evolution of the composite object system (S+P), where S denotes the object system and P the probe system, respectively. Furthermore, denotes the meter observable of the probe (measurement) system, the initial state of the probe system. In case of projective measurements, supposing that the apparatus (or measuring process) M has a family of measurement operators the error can be simplified as . Later it was shown by Hall 4 that these errors correspond to th uncertainty of an estimate of a physical property based on the outcome of an arbitrary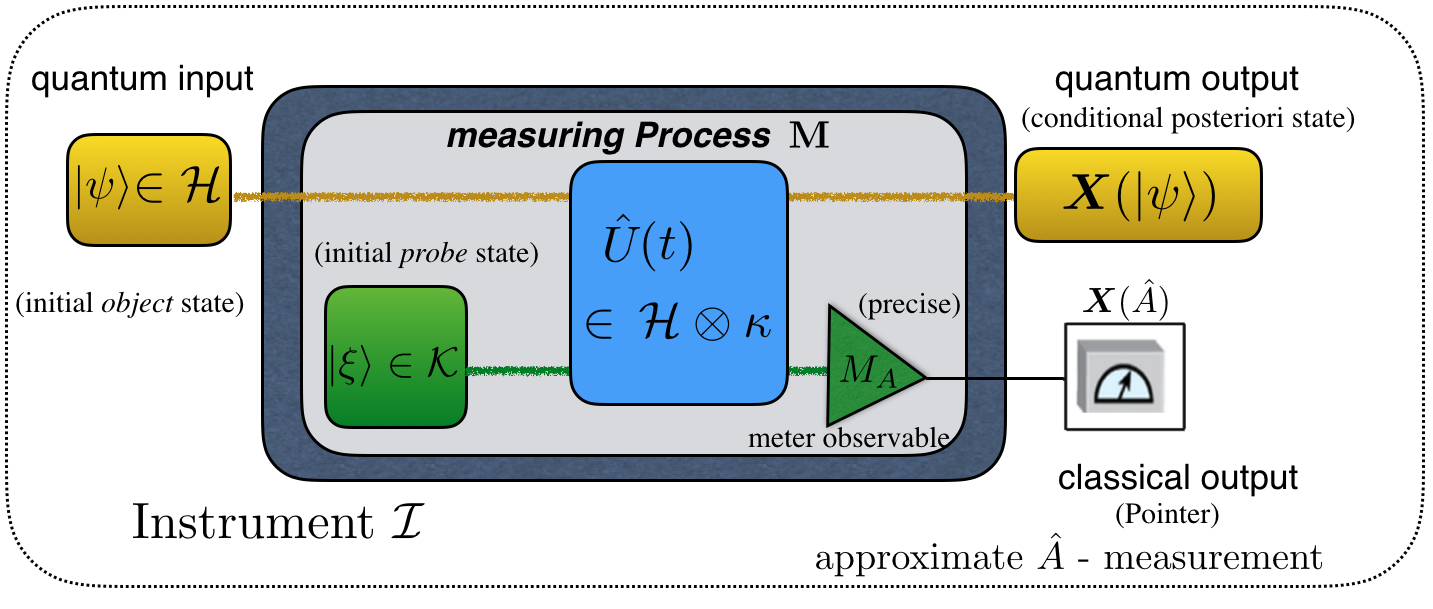 
measurement. In our case the error reads , where the estimated value is given by . As shown by Hofmann 2, this estimate corresponds to a feedback of that can compensate a weak interaction of . The Ozawa-Hall error given above then describes the error of the feedback compensation and can be observed experimentally in the reduction of the spin component from its original value of 1 to . In our experiment, the measurement basis is complete and orthogonal and the operator is self-adjoint. Then the path uncertainty is determined only by the differences between the estimates and the weak values , where denotes the statistical probability in the undisturbed system of finding the neutron in the final state given by . This means, the uncertainty vanishes completely if the compensations applied in the output ports and respectively equal the corresponding weak values . Then the compensations are no longer just estimates of the probe qubit rotations but precisely determine the effects of the weak interactions on each individual qubit. A successful feedback compensation thus realizes a precise evaluation of the weak values. Since the compensation angles can only be real numbers, perfect compensation is only possible if the imaginary parts of the weak values vanish. This can be achieved by adjusting the phase between the two paths to zero.
Then the path presences can be used to correctly calculate e.g. the average spin rotation angle in either context as . And for the uncertainties we get for the which way context and in the interferences context, the same amount of uncertainty . Also the expectation value measured in our experiment depends on the final state. In case we could not distinguish between the two exit beams (have a common compensation angle ), and measure only the averaged expectation value, denoted by in the interference context and in the which-way context as and . In the limit of small both expectation values converge to . Comparing both equations we identify a measurement error of . This means, by not distinguishing between the measurement outcomes we end up with a measurement error equal to the original path uncertainty from before.
Experiment
In the actual experiment we verified the neutron’s presences in path 1, that is . The reduction of is observed when the exit beams are not distinguished. Neutrons are polarized by a magnetic prism which deflects the spin-down neutrons out of the Bragg acceptance angle of the interferometer crystal. The spin rotator DC1 rotates the remaining spin-up neutrons by into the initial state. The spin rotator consists of a DC coil which creates a magnetic field pointing in the y direction. In this region, the spin precesses about the y axis due to Larmor precession within the DC coil. The asymmetry of the 
beam splitter is realized by a partial absorber in path 2. The spin rotations and are realized by small Helmholz coils which modify the external overall guide field such that the spin precession in the xy-plane changes. The precession angle is given by , where is the neutron’s transit time in the magnetic field region, with . To realise the feedback compensation we couple the neutron’s spin weakly to its spatial degree of freedom expressed as . The compensation and the spin analysis is realized only in the forward exit beam, normally corresponding to the state. By changing the phase between the beam paths from 0 to we can however flip the meaning of the exit beams and thereby analyze also the state. The experiment was carried out at the neutron interferometer instrument S18 at the high-flux reactor of the Institute Laue-Langevin (ILL) in Grenoble, France.
i) Which Way Context:
The which-way measurement is described by the observable , i.e., the projector onto path 1. Experimentally the projector is realized by blocking path 2,1, which is schematically illustrated below. Depending on which projection is measured the respective compensation operation is applied, with for path 1 and for path 2. The experimentally observed phase shifts evidently reproduce the theoretically predicted values given by and , accurately yielding and for measurement strength and and for measurement strength , while theory predicts and .
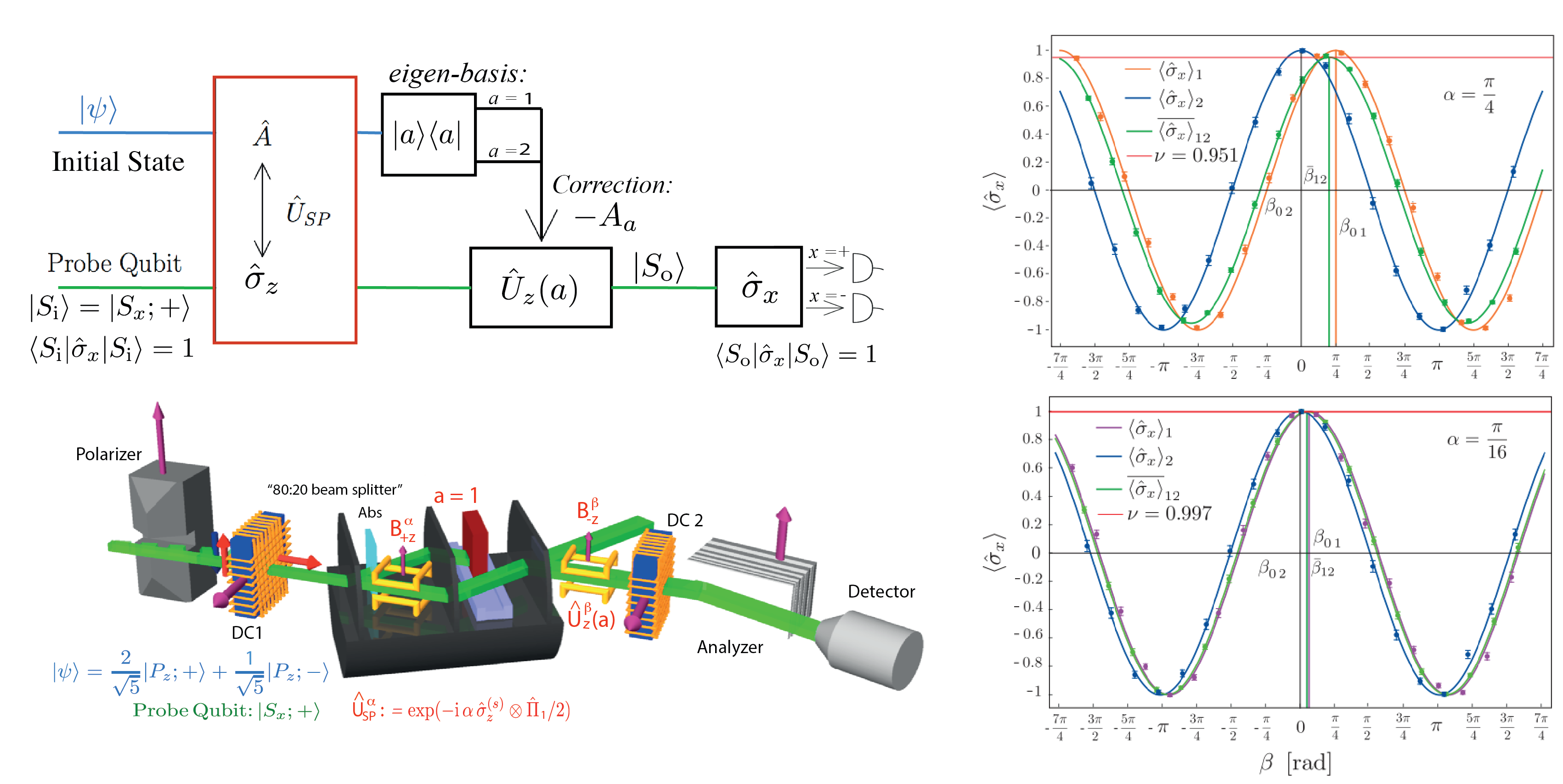
If the same compensation is applied in both paths we observe fringes, shown in green in the figure, which have a reduced visibility of and is determined by the initial path uncertainty . For the two interaction strengths and respectively the theoretical values are and indicated by the red lines in the figure. The experimentally determined values are and . Thus the measured Ozawa-Hall error results in , where theory predicts .
ii) Interference Context:
Regarding the interference context the optimal correction is given by as explained in the previous Sections. Path presences of and , with probabilities and respectively, are obtained in the limit of weak coupling, meaning small values of . Using the setup depicted below, the total combined state, consisting of object system (path) and probe system (spin), behind the phase shifter flag reads with . The experimentally observed phase shifts correctly reproduce the feedback fringes and . In case of the corresponding output port probabilities are and . The fringe shifts are given by . For the predicted values of the path presence are at and at and are evidently reproduced in the experiment as and . The interference context changes the path occupation numbers to and to , with probabilities of and ; for small the experimental results converge on these values as seen from the obtained results and .
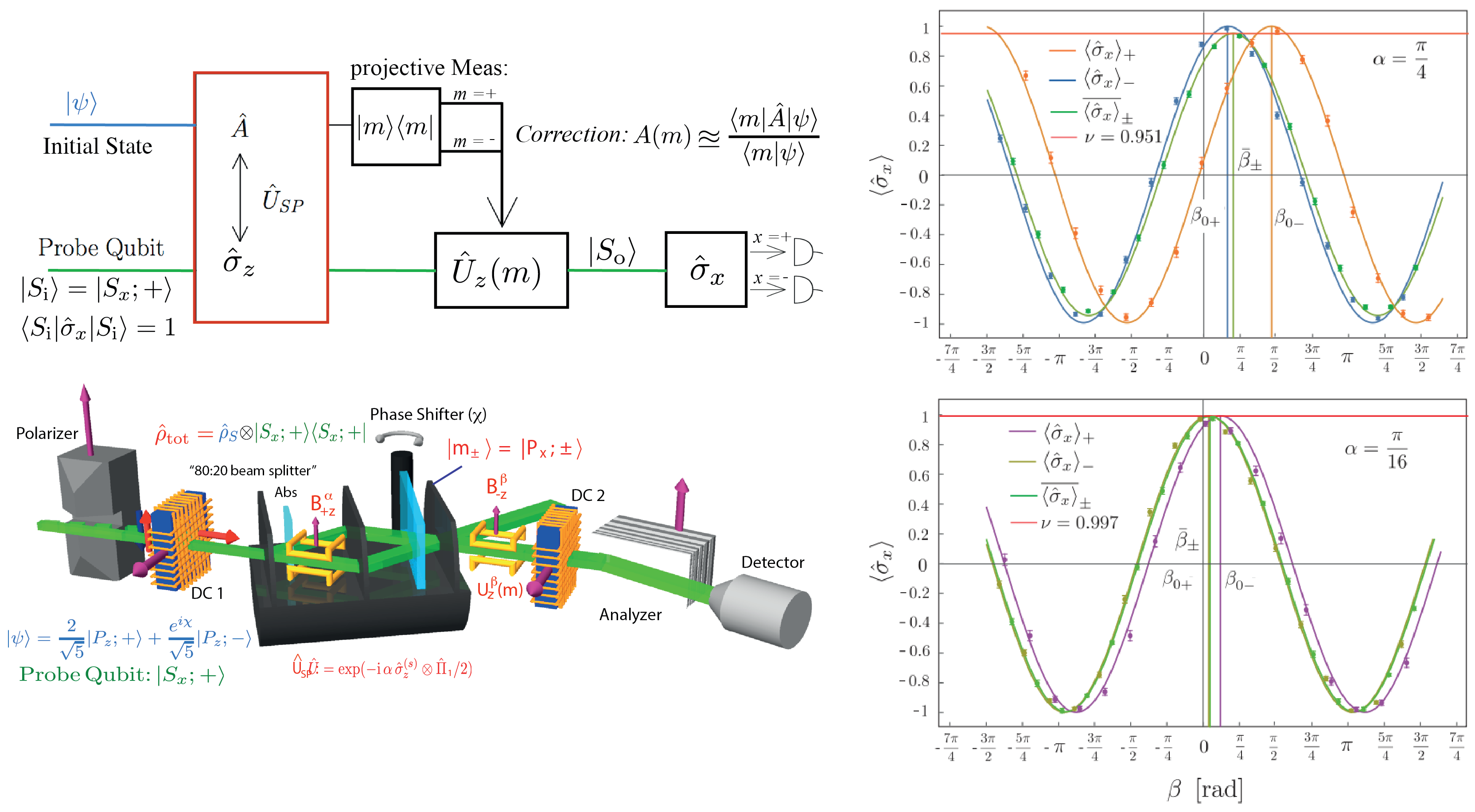
For the chosen wo interaction strengths and again the theoretical values for the visibility are and (indicated by the red lines in the figure) and experimentally determined values yield and , which gives almost the same Ozawa-Hall error as in the which-way context.
A plot of the optimal compensation , accounting for the path presence, versus interaction strength is given aside. The 
measured path presences converge for small towards the weak values. For large , the optimal compensation angle is no longer given by the first order term of but by the complete expression , shown by the dotted line. This change is in principle accompanied by a change in the probabilities of finding the particles in the exits beams, indicating that the probe qubit perturbs the measurement and modifies the output beams in a non-trivial manner. However, the results shown here indicate that this perturbation of the interference effect is sufficiently small in the full range of interaction strengths covered in the present experiment. Our experimental results show that spin rotations applied in one of the paths in a two path neutron interferometer result in proportional rotations of the spin in the output ports of the interferometer. Each of the two different rotation angles observed in the output ports are precisely defined and show no fluctuations. We therefore conclude that the spin rotations define a precise value of the presence of a particle in the path in which the rotation was applied. This result indicates that the particles have a precisely defined fractional presence in the path when interference effects are observed in the output ports.
Now we want to present a direct evaluation of the Ozaw-Hall Error, using the following expression for the square of there error , where denotes the experimentally determined best estimates given by and , obtained for measurement strength . In case of individual “postselection-based” feedback compensation for each output, where theory predicts a vanishing Ozawa-Hall error we get and . When a common compensation of is applied, we obtain and , where theory predicts and , respectively.
To summarise: the precise analysis of the effects of sufficiently small spin rotations applied in only one path of a two path neutron interferometer shows that the presence of the neutrons in the paths during an interference experiment is accurately described by fractional values corresponding to the weak values associated with the output ports of the interferometer, where the precision of the results is given by the Ozawa uncertainties. We have experimentally verified that these fluctuations are close to zero in the present case, providing the first experimental evidence that the partial path presences described by weak values apply to each individual neutron detected in the corresponding output beam of the interferometer. Since this phenomenon is not observed when a which path measurement is performed, our results also demonstrate that the way in which particles propagate through an interferometer depends on the measurements performed in the output. The same initial uncertainty of the particle presence that appears as a statistical distribution of detection events in a which-path measurement will appear as the fluctuation of the partial presence of each individual particle when interference effects are detected instead.
1. Hartmut Lemmel, Niels Geerits, Armin Danner, Holger F. Hofmann, and Stephan Sponar, Phs. Rev. Research 4, 023075 (2022). ↩
2. Holger F. Hofmann, Phs. Rev. Research 3, L012011 (2021). ↩