Optimal compensation angle

We prepare the spin in state and the total initial state reads , with   . We couple spin and path degree of freedom by weakly rotating the spin in path 1. We rotate it by a small angle about the z axis. The rotation is expressed by the operator acting only in path 1 or, equivalently, by the operator acting on the total state of both paths and spin, denoted as  with , where and denote the path projection operators of path 1 and 2 respectively. The state after the spin rotation reads . The states of the two exit beams of the interferometer are given by the projection onto the exit states denoted as . The respective compensated state are . Rewriting the operators as we get , where and denote the weak values of the path projection operators respectively with and .

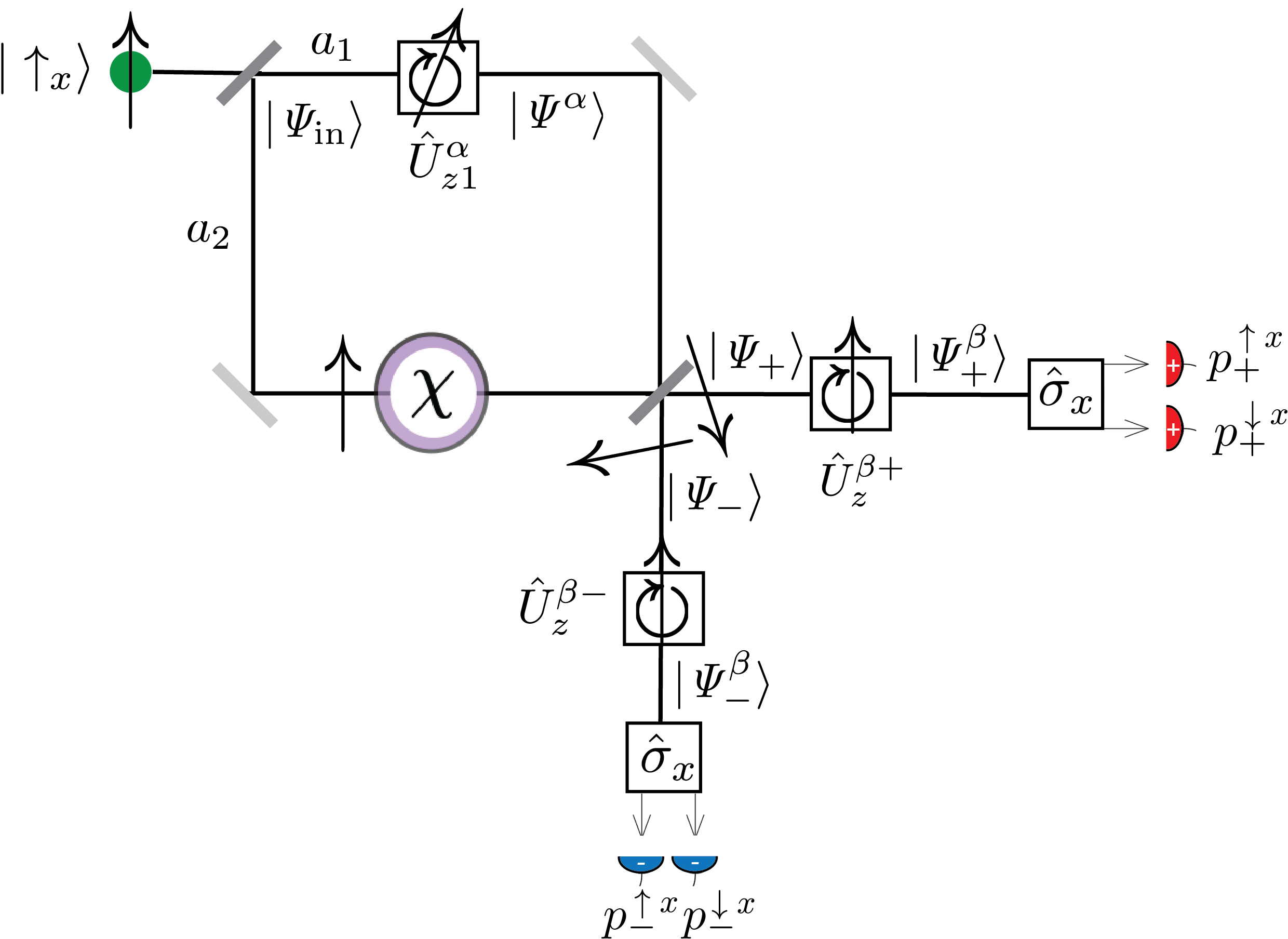
The read out the probe qubit is achieved by factorising the state in each port into the path dependent and a spin dependent part as , with . Now we can calculate the amplitudes of the eigenstates of the spin qubit as and . For the amplitude vanishes and the final spin state equals the initial state . Since we focus only on the limit of a small interaction strength series expansions gives . Simply speaking, in the limit of weak coupling, that means small values uf , the weak value of the path projection operator is given by the ratio of the spin rotation angle and the optimal compensation as – this ratio of angles is our new experimental accessible quantity, which we refer to as path presence.