Direct Path State Characterization by strongly measuring Weak Values

Quantum state tomography (see here for details) is the process of reconstructing, or more precisely completely characterizing, the quantum state of an object which is emitted by a source. This technique has become an essential tool in the emerging field of quantum technologies, such as quantum communication or quantum computing. The theoretical framework of quantum state tomography dates back to the 1970s, and experimental implementations are nowadays routinely carried out in a wide variety of quantum systems. The basic principle of quantum state tomography is to repeatedly perform measurements from different spatial direction – on the quantum systems in order to uniquely identify the system’s quantum state. Nevertheless, for quantum state tomography a lot of computational post-processing of the measured data is required to deduce the initial quantum state from the observed measurement results – all together a high expenditure.

Consequently, in 2011 a novel, more direct tomographical method was established that makes it possible to determine the quantum state without the need for post-processing ¹. However, that novel method had a major drawback: it uses minimally disturbing measurements, so called weak measurements, to determine the system’s quantum state. The basic idea behind weak measurements is to gain very little information about the observed system, by keeping the disturbance on it, caused by the measurement process, (negligible) small. Since the amount of information that is gained in this procedure is very small the measurements have to be repeated many many times – a huge disadvantage of this measurement procedure in practical applications. Now we managed to combine these two methods and got the benefits from both of them. We were able to further develop the method established in 2011 in such way that the need of computational post-processing becomes obsolete, as proposed recently in ².

Our measurement scheme ³ starts with the initial state , where is the initial path and the initial spin state. and are the eigenstates of path  and  respectively, with the corresponding probability amplitudes and . denotes a spin state that is aligned along the positive -axis. A general form for a pre-selected path state is given by , where represents the relative phase and the weight of the two eigenstates (the probability amplitudes   and   are linked to the general state by   and  ). Note that at this point we have no coupling between the spin and path degree of freedom – the system is in a completely separable state. Next a coupling is created by a unitary evolution consisting of path dependent spin rotations:the spin is rotated by a certain angle around the -axis in the -plane with positive (clockwise) rotations in path and negative (counter clockwise) ones in path . The corresponding interaction Hamiltonian is given by , where are the projection operators on the path eigenstates and , , where is the neutron’s magnetic moment and are the Pauli spin matrices and the applied magnetic field. The evolution of the composite system  is described as . The angle of rotation is given by , here is the neutron’s transit time in the magnetic field region. In our experiment represents the relevant parameter for the interaction strength of the measurement. In the standard weak measurement procedure the evolution operator is series expanded around and by neglecting higher order terms of an approximation for is made (see here for theory). Here, however, the analytical relation  is  applied and hence no approximation is made. Therefore the calculations hold for arbitrary interaction strengths. In a last step the past is post-selected on the final state . Applying the setup, schematically illustrated below, projective measurements along the six spin directions , and are performed, yield six intensities with , which allow us to extract the imaginary and real part as well as the modulus of the path operator’s weak value expressed as ,  and .

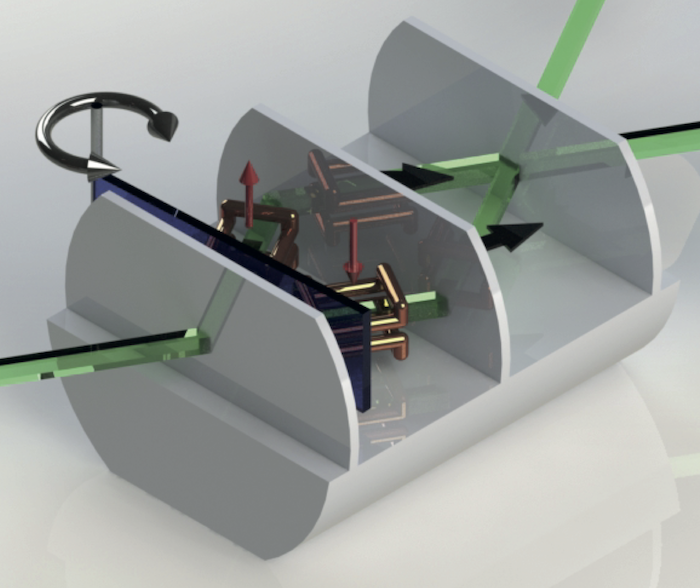
Schematic drawing of the experimental setup: Magnetically birefringent prisms are used to separate the spin up () and down component () to polarize the neutron beam, due to absorption of the spin down sub-beam using Cadmium (Cd). A DC coil brings the neutron spin from the +z to the +x state. This completes the preparation of the initial spin state. Upon the first plate of the interferometer the neutron beam is split along two paths. A sapphire slab is used to tune the relative phase between them. Small coils in Helmholtz configuration in each path make it possible to rotate the neutron spin in the xy-plane. At the third plate of the interferometer the beams are recombined. Finally a second DC coil mounted on a translation stage in combination with a polarizing supermirror are used to perform the spin analysis.

Since , the complete determination of the weak value of the Pauli operator also gives the weak values of the projection operators on each path eigenstate, which in turn characterize the measured pre-selected path state  from above:

the probability amplitudes of are given by and . They are directly proportional to quantities that are determined experimentally, namely to the path projection operators’ weak values. The intensities recorded in our experiment, completely determine . Using the weak values of the path projection operators and are calculated, which in turn are directly related to the preselected path state, making available. The results of such a direct state characterization for weak () and strong () measurements are shown below:

Our results give clear evidence  that strong interactions outperform weak ones for tomographic accuracy. Strong interactions are superior in terms of accuracy (a measure of deviation from the theoretical prediction) and precision (a measure of fluctuation), as well as required measurement time. Our results are not limited to neutron interferometry, but can be used in many n-dimensional quantum systems. A final remark – our work was selected as a scientific highlight  in the 2017 ILL annual report.

1. J. S. Lundeen, B. Sutherland, A. Patel, C. Stewart, and C. Bamber, Nature (London) 474, 188 (2011). ↩

2. G. Vallone and D. Dequal, Phys. Rev. Lett. 116, 040502 (2016). ↩

3. T. Denkmayr, H. Geppert, H. Lemmel, M. Waegell, J. Dressel, Y. Hasegawa, and S. Sponar,
Phys. Rev. Lett. 118, 010402 (2017) [quant-ph/1604.04102]. ↩