Spin-Rotation Coupling

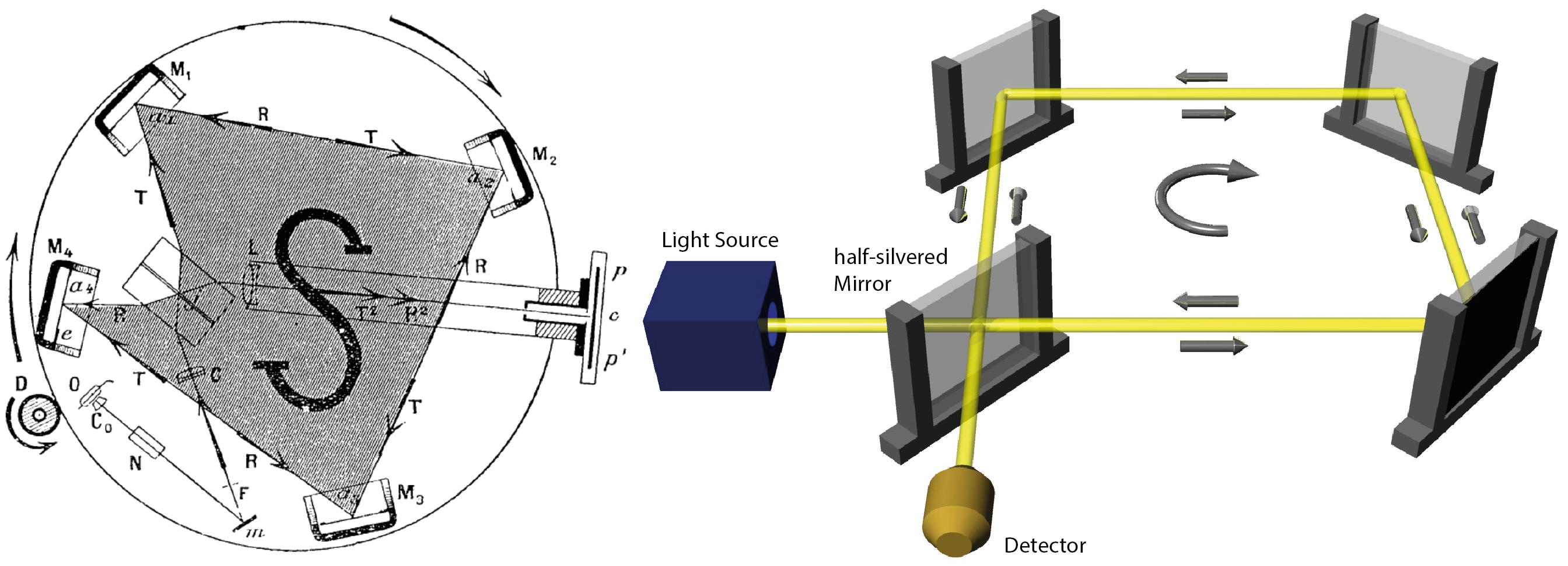
Influence of rotation on the phase of light passing through an optical interferometer has been theortically investigated over a century. The Sagnac effect, named after French physicist Georges Sagnac, that is the observation of a phase shift proportional to the scalar product of the rotation frequency and the area of the interferometer ¹ provided an empirical basis for a rich field of both fundamental and apptied research into the influence of rotation on the phase of a quantum mechanical wave function. Sagnac’s original drawings (left) and a schematically illustration of the rotating interferometer (right) are depicted below.

In order to calculate the phase shift of our Sagnac interferometer consider a circular interferometer of radius , illustrated below, rotating in its plane at an angular frequency . The time taken for the two beams (of particles) to complete one circuit of the interferometer, , is calculated as , where  is the speed of propagation of our particles around the Sagnac loop. Thus we get  and therefore .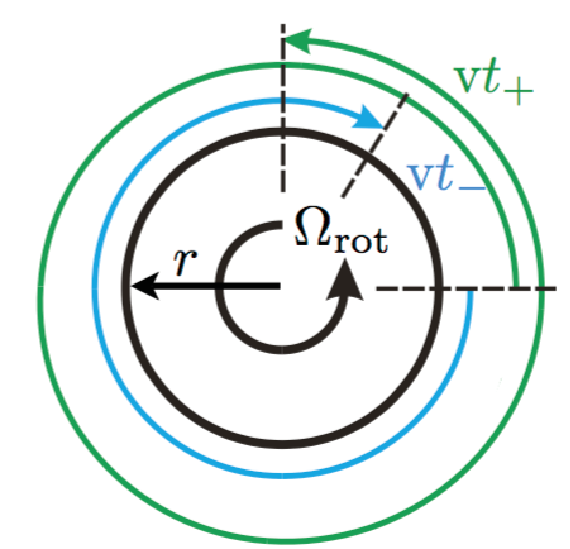 It follows that the difference in propagation time for the two counter-propagating beams, , is given by  . The area of the interferometer is  and in most case one can assume  . So for the phase difference, given by we finally get (in 3 dimensional space) , where is a unit vector perpendicular to the surface area of the interferometer. If we now go back to a interferometer in form of a square (middle) the relative phase difference increases (at first order) by a factor and we get . In the case of light we have and and the relative phase difference is expressed as . The Sagnac effect may be regarded as a manifestation of the coupling of orbital angular momentum of a particle, , to rotation. The Sagnac phase shift, as defined above, is a scalar quantity that is independent of the motion of the observer.

From the standpoint of a rotating observer, may naturally be extended to include the intrinsic spin of a quantum mechanical particle through replacing the orbital angular momentum with the total angular momentum . This fomalism consequently predicts that in the rotating frame, in addition to the Sagnac phase shift, a displacement of the interference fringes due to spin-rotation coupling will arise proportional to , as explicitly expressed in the first Equation in the paper by Bahram Mashhoon ². For a deeper understanding of the spin-rotation coupling an extension of the hypothesis of locality is used to determine the interference phase shift induced by the rotation of a neutron interferometer. The basic laws of physics are formulated with respect to ideal inertial observers. However, all actual observers are accelerated (eg. rotation of the earth). To interpret the 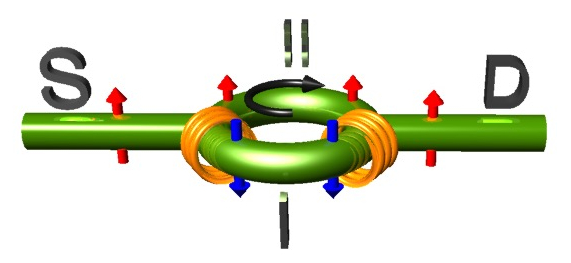results of experiments, it is therefore necessary to establish a connection between actual and inertial observers. This is achieved in the standard theory of relativity by means of the hypothesis of locality, namely, the assumption that an accelerated observer at each instant along its worldline is physically equivalent to an otherwise identical momentarily comoving inertial observer. Consider a particle of energy and momentum with respect to an inertial frame , having coordinates , and a frame , with coordinats  that is related to by a uniform rotation of angular frequency . An observer at rest in with velocity with respect to measures the energy of theparticle. According to the hypothesis of locality, the result is , where  and  , which can be rewritten as , since  and is the orbital angular momentum of the particle. For a general Hamiltonian this reads  . The hypothesis of locality is thus valid for phenomena involving classical particles. 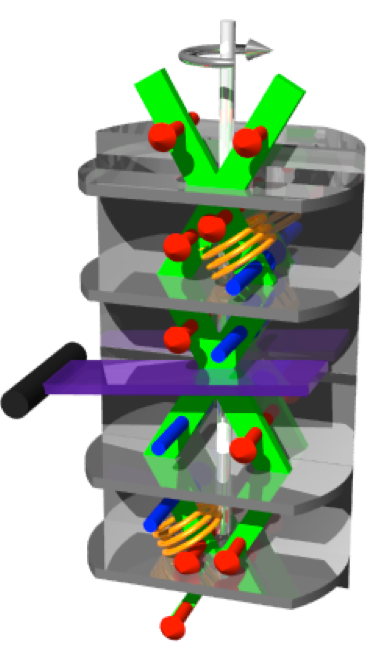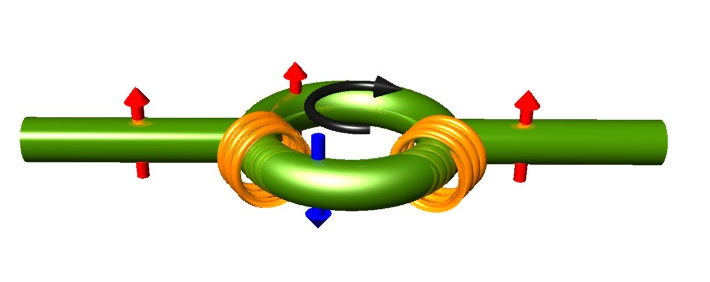However, (matter) wave properties in quantum mechanics, such as period and wavelength, require extended intervals of time and space, respectively, for their determination. It is therefore necessary to develop a prescription for the measurement of wave characteristics by accelerated observers. A generalization of the hypothesis of locality can be stated as follows: A wave function  with respect to a static observers in , is represented as the wave function in the uniformly rotating frame as , where  is a unitary operator given by , where is the total angular momentum, consisting of orbital and spin angular momentum, denoted as  . The wave function satisfies the Schrödinger equation  such that wave function satisfies the Schrödinger equation  with . A detailed comparison of the last equation with  reveals,  the existence of a new effect associated with the coupling of intrinsic spin with rotation and given by the Hamiltonian . It is interesting to investigate the observational consequences of the new effect given by the last equation with polarized neutron interferometry ³. The proposed experimental realization for observation of the spin-rotation coupling is illustrated above (left). Neutrons coming a source (S) are split into identical semicircular beams which are then made to interfere before being detected at D. Along the counterclock-wise (clockwise) path, the neutron spin is assumed to be polarized parallel (antiparallel) to the direction of rotation of the interferometer. The wave function at the detector (D) is simply given by . The interference phase shift (in the quasi classical approximation) is given by , where and is the difference between the phase of the neutron wave at the detector at time and the phase at the source at time , with . Here is the neutron group speed in the inertial frame and is the radius of the interferometer. This can be calculated to first order in resulting in two parts , where , with neutron mass and being the arera of the interferometer, and . The 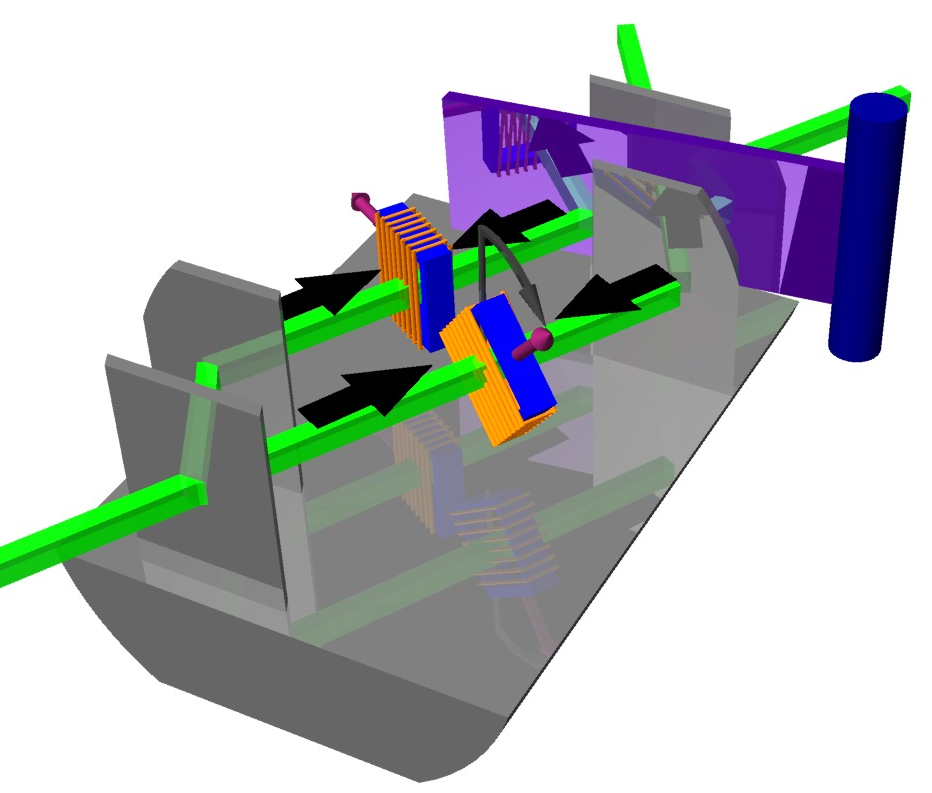latter effect, is smaller than the Sagnac effect by the ratio of the (reduced) de Broglie wavelength of the neutron to the diameter of the interferometer, . The Sagnac effect is proportional to the area of the interferometer, whereas the spin-rotation coupling phase shift is proportional to the length of the separate neutron paths. The Sagnac term has already been observed in experiments at the University of Missouri-Columbia ⁴ and MIT ⁵. Since the spin-rotation coupling on the neutron phase shift is very small and to separate it from the much larger Sagnac effect it would require a very sensitive interferometer. To overcome this difficulty, Sam A. Werner has proposed an experiment using a new type of interferometer which ideally would be insensitive to Sagnac (and other gravity effects), which  is illustrated aside (right). In ² Bahram Mashhoon proposed a setup where in a neutron interferometer longitudinally polarized neutrons pass through a slowly rotating spin flipper (instead of the interferometer itself) along one arm and a static spin flipper along the other arm resulting in a beat phenomenon at the detector, which is illustrates on the left side. Keeping the interferometer stationary in the inertial frame of the laboratory, then rotating one of the coils with angular velocity parallel to the neutron wave vector. Then a shift in frequency of this beam will induce a time-dependent interference intensity envelope of the form arises, where  is the  phase shift due to the phase flag. Finally Bahram Mashhoon proposed to replace the rotating spin-flipper by a stationary quadrature coil, which produces a rotating magnetic field , normal to the polarization axis of the neutrons ⁶. The expected result should be the same, since the neutron cannot distinguish if the flipper is physically rotated or the magnetic field is rotated.

To describe the interaction of the spin of a free neutron in a magnetic field with angular velocity the Pauli–Schrödinger equation has to be solved for a particle propagating in −direction in a uniformly rotating magnetic field given by which gives  (see here for details of the derivation). The Pauli equation in a rotating magnetic field for plane waves is analytically solvable and in this particular case given by , where generates the rotation of the initial spin state ,  which cab be expressed as  . The square of the magnitude of the rotation vector is given by a Pythagorean equation , where we used the definition of the Larmor frequency . The solution from above contains the coupling term and describes the evolution of the spin states for both the rotating and the static field ().

1. Georges Sagnac, CR. Acad. Sci. (Paris), 157, 708 (1930). ↩

2. Bahram Mashhoon, Richard Neutze, Mark Hannam, Geoffrey E. Stedman Phys. Lett. A, 249, 161 (1998). ↩

3. Bahram Mashhoon, Phys. Rev. Lett., 61, 2639 (1988). ↩

4. S. A. Werner, J.-L. Staudenmann, and R. Colella, Phys. Rev. Lett., 42, 1103 (1979). ↩

5. D. K. Atwood, M. A. Horne, C. G. Shull, and J. Arthur, Phys. Rev. Lett., 52, 1673 (1984). ↩

6. Bahram Mashhoon and helmut Kaiser Physica B, 385, 1381 (2006). ↩