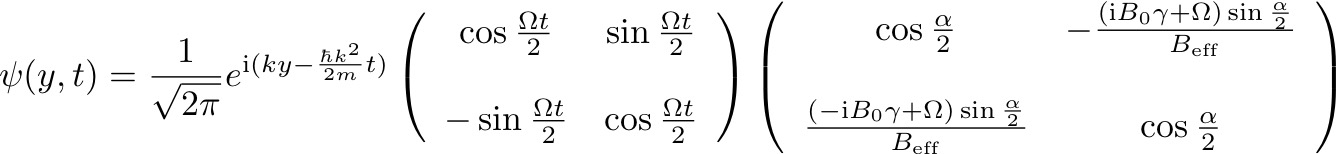The Neutrons’ Interaction in a uniformly rotating magnetic Field

This page describes in detail the derivation of the analytic solution of the wave function for a neutron in a uniformly rotating magnetic field. For a uniformly rotating magnetic field , and a particle moving into the y – direction the Schrödinger equation (Pauli equation) is given by . Using the separation ansatz we get the following two (seperated) differential equations . The solution of the right side for a plane wave moving into the +y direction simply yields , with , while the differential equation of the time dependent spinor gives Applying following substitution transforms the last equation into a homogeneous differential equation . To solve this equation we perform a transformation onto the rotating frame by the following unitary operation , which yields and multiplying from the left side with finally yields , where we used . Using the definition of the Larmor frequency and rearranging the terms leads to the following equation . This equation can be integrated, giving the following solution , where is the rotation vector, is the magnitude and the unit vector of the rotation. Undoing the previous transformation, the time evolution of the spin in this uniformly rotating frame is given by and finally the wave-function consiting of spinor and spatial part is given by . Using the identity the matrix representation of the wave-function can be written as