4π Spinor Symmetry in Interferometry and Geometric Phases for maximally mixed States using 3D printed Larmor Spin Rotators

In our latest neutron optical experiment ¹, we developed a method for coherent Larmor spin-rotation control using topology-optimized 3D-printed magnets for applications in neutron-interferometer experiments, where the rotation axis is parallel to the outer guide field. The magnetic action can be adjusted linearly by varying the distance between the magnets. We show that spin-rotation angles of more than 4 are possible, depending on the initial magnetization strength. The measurements are in good agreement with the simulations and show a spin contrast of more than 95%, comparable to older methods using Helmholtz coils. The advantages of this method are that unwanted inductances are avoided and that no heat is dissipated by current-carrying wires, which prevents a reduction in interferometric contrast due to temperature gradients or would make water cooling necessary. In general a Larmor spin rotator must have a highly homogeneous field along the neutron-beam path, because an inhomogeneous field would lead to a dephasing of the neutron and therefore to a loss in contrast (fringe visibility) of the interferogram. Another crucial point is the thermal stability of the setup. A change of temperature during the measurement leads to a loss in contrast, as phase drifts occur, e.g., a temperature change of 1°C results in a 1.92 rad phase shift, as depicted aside. For this reason, the Helmholtz-coil Larmor spin rotators, usually applied in our experiments, are water cooled, which complicates the setup of the experiment because the temperature of the cooling water has to be optimized. In addition, the manufacture of waterproof boxes to hold the Helmholtz coils is tedious. Before we go into details of the designs of our new topology-optimized 3D-printed magnets, we want to introduce the procedure of magnetic 3D printing.

Production of 3D-printed Magnets:

In a cooperation with the group of Dieter Süss (Physics of functional materials) from the faculty of physics, university of vienna where they operate a Christian Doppler lab. This group demonstrated recently that an end-user 3D printer can be used to print polymer-bonded rare-earth magnets with a complex shape: thermoplastic feedstock, in the form of a wire filament, is a common base material for 3D printing. These filaments are available with different properties that require appropriate printer parameters, for example temperature or printing speed. Commercial filaments are available with diameters of 1.75 and 2.85 mm (see for example Innofil3D  a subsidiary company of BASF). However, filaments with permanent magnetic properties are currently not commercially available. Consequently, the prefabricated compound material Neofer~25/60p from Magnetfabrik Bonn GmbH was used to develop a new printing material. This polymer-bonded magnetic compound consists of a polyamide matrix (PA11) and the magnetically isotropic NdFeB powder MQP-S-11-9 from Magnequench Corporation. It is processed into printable filaments with the powder making up 85\% of the final product by weight. These magnetic filaments can be printed using a low-cost Fusing Deposition Modeling (FDM) 3D printer.A maximum printing temperature of 260°C, and a nozzle diameter of 0.4 mm are used. Structures with layer heights between 0.05 and 0.3mm are printable with our setup and polymer-bonded rare-earth magnets with complex shapes can be manufactured. See the picture aside for a photograph of the printer and a scanning electron microscope (SEM) image of a filament. Detailed investigations of the magnetic properties of the material used can be found in the following publication ².

Design of the 3D-printed Larmor Spin Rotators

The volume, where the homogenous static magnetic field shall be present is simplified by a fieldbox with a size of 7 x 7 x 40 mm . In order to describe the influence of the magnetic field on the phase shift of the neutrons, the action is defined as . In order to rotate the spin of a neutron with a wavelength of Å by an angle , an action of 35 mT mm is required. The action , of a simplified Helmholtz-coil geometry (only a single winding), using the finite-element-method (FEM) tool MAGNUM.FE, as a function of the current can be seen aside. Now the goal is to find an optimized permanent-magnetic Larmor spin rotator by the usage of the inverse-stray- field and topology-optimization framework, based on the following design parameters: i) Size of the field box is 7 x 7 x 40 mm . ii) Maximum design volume   is  24 x 24 x 20 mm . iii) Action  is 35 mT mm. vi)   is adjustable in the range  mT mm. v) Homogeneous magnetic field density . A challenge for a permanent-magnetic system is the possibility to make the action adjustable. In the case of the Helmholtz-coil geometry, this is simply achieved by changing the current through the coils. Thus, the straight forward way to adjust for a permanent-magnetic setup is to change the distance between the neutron path (field box) and the magnets. Aiming to realize a homogeneous magnetic field density in the field box , the components of along the and directions must be zero. For the component, only the gradient along and must be zero. This design parameter is implemented in the minimization algorithm as the following objective function: , being the quadratic sum of all undesired field gradients.

Two different initial designs are investigated to find a proper replacement of the Helmholtz coils: the first design is a modified Halbach cylinder (depicted left above) and the second investigated design is a topology-optimized approach (right), where the mesh of the design domain consists of 256 542 tetrahedral elements. The homogeneity of inside the field box has a crucial impact on the performance of the neutron optical device. Thus, serving as a measure of performance, the relative error is defined as . Plotted aside you can see the action as a function of the gap , with =61 mT for the topology-optimized design and = 68 mT for the Halbach cylinder, and also as a function of the remanence of the magnet (gap z=2mm). Next we take a look at relative error as a function of the gap z for the relative error as a function of the action for the optimized designs and for the current Helmholtz-coil geometry.

Finally, the topology-optimized version shows a smaller relative error , which leads to a more homogeneous action across the beam profile in neutron-interferometer experiments, which in turn gives a better contrast. Consequently the  topology-optimized design approach prevailed. The  topology-optimized approach consist of  four segments of the same shape, which is illustrated below. Each of the four segments must have a remanence of exactly = 61 mT to generate an action of =  35 mT mm for a gap of z = 2.25 mm. Now a  jig with the exact positions of the segments is 3D printed, using the filament Neofer~25/60p (introduced above). Magnetization of the segments is achieved by using an electromagnet in permanent-operation mode.  The jig is inserted into the electromagnet and the external field is increased in small steps, where after each step, the magnetic field density of the segments is measured by the 3D Hall probe. A comparison between the simulation and the actual measured magnetic field, together with a photo of the four segments can bee seen below. The magnetic field vectors are color encoded the following way:  blue -> coil simulation, red -> topology- optimization simulation and finally  yellow -> actual measurement). These vectors clearly illustrate the homogeneity of the applied magnetic field. The line scan of is done at y=0 mm and z=0 mm.

Polarimetric Test Setup for Spin Flip:

Of course, the actual performance of the 3D-printed Larmor spin rotator can be only tested with a neutron experiment. For this reason, first test measurements with neutrons are performed at  the polarimeter instrument NepTUn (NEtron Polarimeter TU wieN), located at the tangential beam port of the 250kW TRIGA research reactor at the Atominstitut – TU Wienin Vienna, Austria. The test setup is depicted below. In order to control the position of the magnets relative to the beam, they are placed in a specially designed holder that was 3D printed using a commercial synthetic polymer filament (Ultimaker ABS Acrylonitrile butadiene styrene, 2.85mm). The distance between the magnets is adjusted by moving the two sections of the holder relative to each other, using an Arduino-driven stepper motor. The complete setup consist of the following components: By spin dependent refraction from magnetic multilayer structure (hence on refereed to as  supermirror) the incoming neutrons are polarized along the +z-direction. Next a direct current coil (DC-1) rotates the polarization along the y-axis (flight direction), where the polarization vector now precessed in the static magnetic guide field of 1.3 mT, before the neutrons reach the 3D-printed  topology-optimized spin flipper. This first measurements – spin flip configuration – for a gap of   = 2.25 mm with the original remanence of = 61 mT, yielding an action =  35 mT mm, resulting  in a spin rotation of , that is a spin flip. Next DC-2 coil performs a π/2 flip around the x-axis to produce a spin component in the z direction. This component is analyzed by the supermirror, which allows only neutrons polarized in z direction to pass to the detector. By varying the distance of DC-2 (again using a stepper motor), different total precession angles are selected. A modulation of neutron intensity in the detector is observed as a function of this distance. This signal is recorded with (red curve) and without (blue curve), yielding a phase difference of ° was obtained.

Polarimetric Test for arbitrary spinor rotation angle:

After this first successful test of a 3D-printed  topology-optimized spin flipper the next goal is to test the full potential of the tunability of the device. Therefore, the procedure from above is repeated for different values of the gap and the spin rotation angle  is deduced from the obtained intensity oscillations. These measurements show such a promising linearity of the phase shift with (left), that the 3D-printed magnets are magnetized to a four times higher remanence of   = 244 mT (right), in order to have a wider tuning range of the spin-rotation angle .

Later polarimetric measurements with four times higher remanence = 244 mT. The spin-rotation angle of the measured interference patterns calculated from sine fits against the magnet distance . Again intensity oscillations for different gap sizes are obtained by translating DC2 along the beam.

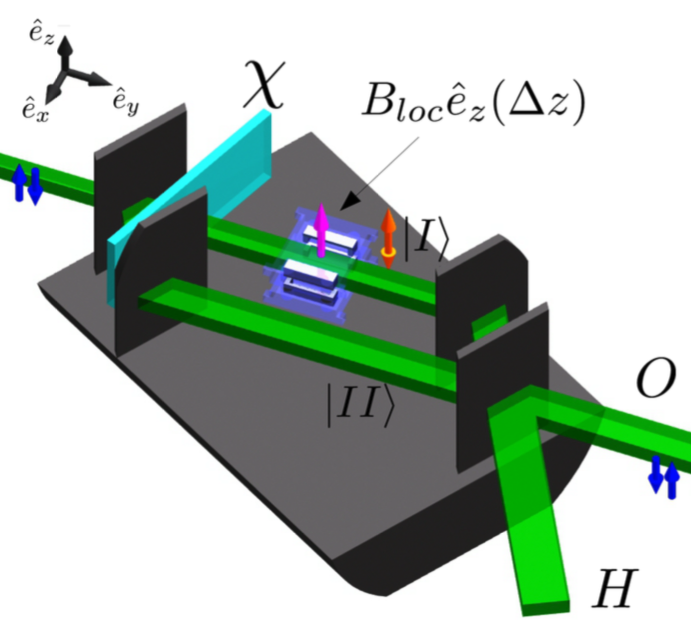
Interferometer Setup to test 4π Spinor Symmetry :

To demonstrate the full potential of the newly fabricated 3D-printed spin rotators they are placed inside a perfect-crystal neutron interferometer. The experiment is comparable to the historic first demonstration of the 4π-spinor symmetry, which was also measured at the Atominstitut already in 1975 ³. The unpolarized neutron beam, owing a cross section of 10 × 10 mm is coherently split into paths and at the first interferometer plate. The phase-shifter plate is rotated in order to create a phase difference between the two paths. Due to the change of the relative path length within the phase shifter slab for path I and II different phase contributions are accumulated from the interaction with the phase shifter’s nucleus for path I and II, respectively. The 3D-printed Larmor spin rotator with variable z is placed in path I. At the last interferometer plate, the two paths are recombined and leave the interferometer in two separate beams, the O beam in the forward direction and the reflected H beam.  The O-beam intensity of an empty interferometer as a function of  is expressed as , where, is an parameter and depends on the interferometer used, temperature gradients, vibrations, etc. The density matrix of an unpolarized neutron in the interferometer, assuming perfect contrast C = 1, is denoted as the direct product , where the first term in the product is the path state , which depends on the phase shift and the second term is the maximally mixed spin state.  The interaction with the local magnetic field in path I is described by the unitary evolution , denoted as , where depends on . At the last interferometer plate, the projector acts on the path state and projects it onto the state . Thus, the intensity at the O detector is given by , where the empirical pre-factor has been reintroduced in front of the interference term. The experimental sedtup is schematically illustrated below on the left side.

The contrast  approaches zero for odd multiples of the spin rotation angle , i.e., when the spin states in the two paths are orthogonal. At the interferogram exhibits a phase shift of compared to , that is with magnets removed. Only at the interferogram has returned to its initial contrast and phase, which shows the -symmetry of the neutron as a spin-1/2 particle.  For an experimental demonstrate this spinor-symmetry in a neutron interferometer experiment, three different magnetization strengths of the 3D printed Larmor spin-rotator are used, each indicated by the magnetic field strength measured in the center point at mm. Measurements of the dependence of the magnetic field on the distance are plotted below left. Below on the right side the results of the interferometric measurements are depicted, which evidently reproduce the -symmetry in the experiment.

Geometric Phases for maximally mixed States :

Finally, we want to emphasize that the curve on the Bloch sphere traced out during the evolution subtends a geodesically closed solid angle . Hence, two pure states   acquire a geometric phase . For a general mixed state we obtain , with respective contrast (visibility) , which reduce to the usual expressions for pure states when letting  ⁴. In the case of maximally mixed states (as we have it in our case) we get and , yielding an output intensity of , which is equivalent to our experimentally obtaoined intensity from above. This eqiation shows that in our experiment the sign change for is a consequence of the phase shift .

Future Perspectives

Another interesting field configuration is that of a wiggler, that consists of stacked regions of antiparallel magneticfields along the beam path. The spatial variation of the magnetic fields in the wiggler leads to resonant Rabi flops of the spin, similar to the working principle of a resonant-frequency spin flipper, where the variation happens in the time domain. Using such devices, once could think of the possibility to shape the beam profile in momentum space. The Larmorspin-rotator design developed in this work can be seenas a first step toward an implementation of custom magnetic field shaping using 3D-printed permanent magnets inneutron optics.

1. W. Kersten, L. Brandl, R. Wagner, C. Huber, F. Bruckner, Y. Hasegawa, D. Suess, and S. Sponar, Additive-Manufactured and Topology-Optimized Permanent-Magnet Spin Rotator for Neutron Interferometry, Physical Review Applied 12, 014023 (2019). ↩

2. C. Huber, C. Abert, F. Bruckner, M. Groenefeld, O. Muthsam, S. Schuschnigg, K. Sirak, R. Thanhoffer, I. Teliban, C. Vogler et al., 3D print of polymer bonded rare-earth magnets, and 3D magnetic field scanning with an end-user 3D printer, Applied Physics Letters 109, 162401 (2016). ↩

3. H. Rauch and A. Zeilinger and G. Badurek and A. Wilfing and W. Bauspiess and U. Bonse, Verification of Coherent Spinor Rotation of Fermions, Phys. Lett. 54A, 425 (1975). ↩

4. E. Sjöqvist, A. K. Pati, A. Ekert, J. S. Anandan, M. Ericsson D. K.L. Oi, and V. Vedral, Geometric Phases for Mixed States in Interferometry, Phys. Rev. Lett. 85, 2845 (2000). ↩

5. G. Badurek, Ch. Gösselsberger, E. Jericha, Design of a pulsed spatial neutron magnetic spin resonator, Physica B 406, 2458 (20002011a>. ↩