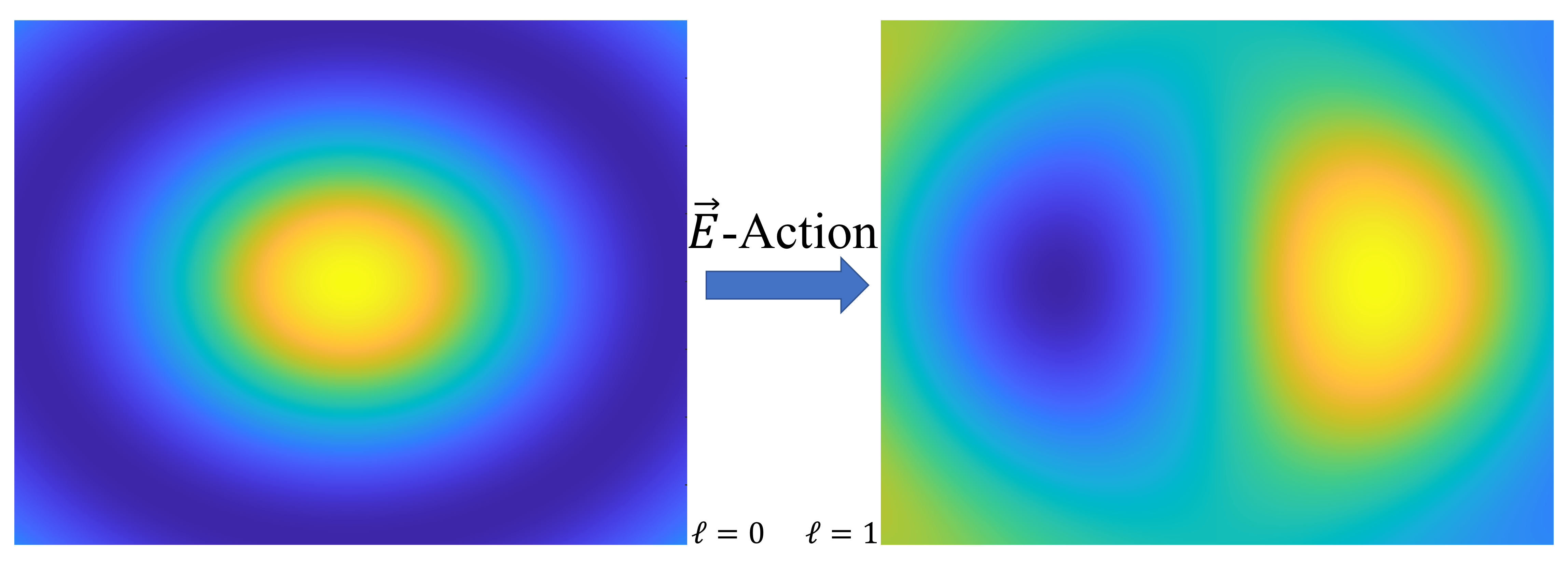
Here we show the cross-section of two Eigenstates of the cylindrical Schroedinger equation, one without orbital angular momentum and one with one unit of orbital angular momentum (see here for details of theory).

Perhaps more surprising is our prediction of so called transverse spin-orbit states, where the or- bital angular momentum of the neutron is oriented transversly to the propagation direction. This can be realized with an electric field oriented perpendicularly to the propagation direction of the neutron. In practice this coupling is much more pronounced than the longitudinal variant, since the electric field now couples to the longitudinal wavevector, which is usually 3-4 orders of magni- tude larger than the transverse wavevector. Transverse orbital angular momentum has not been explicitly observed in any particle system to our knowledge.

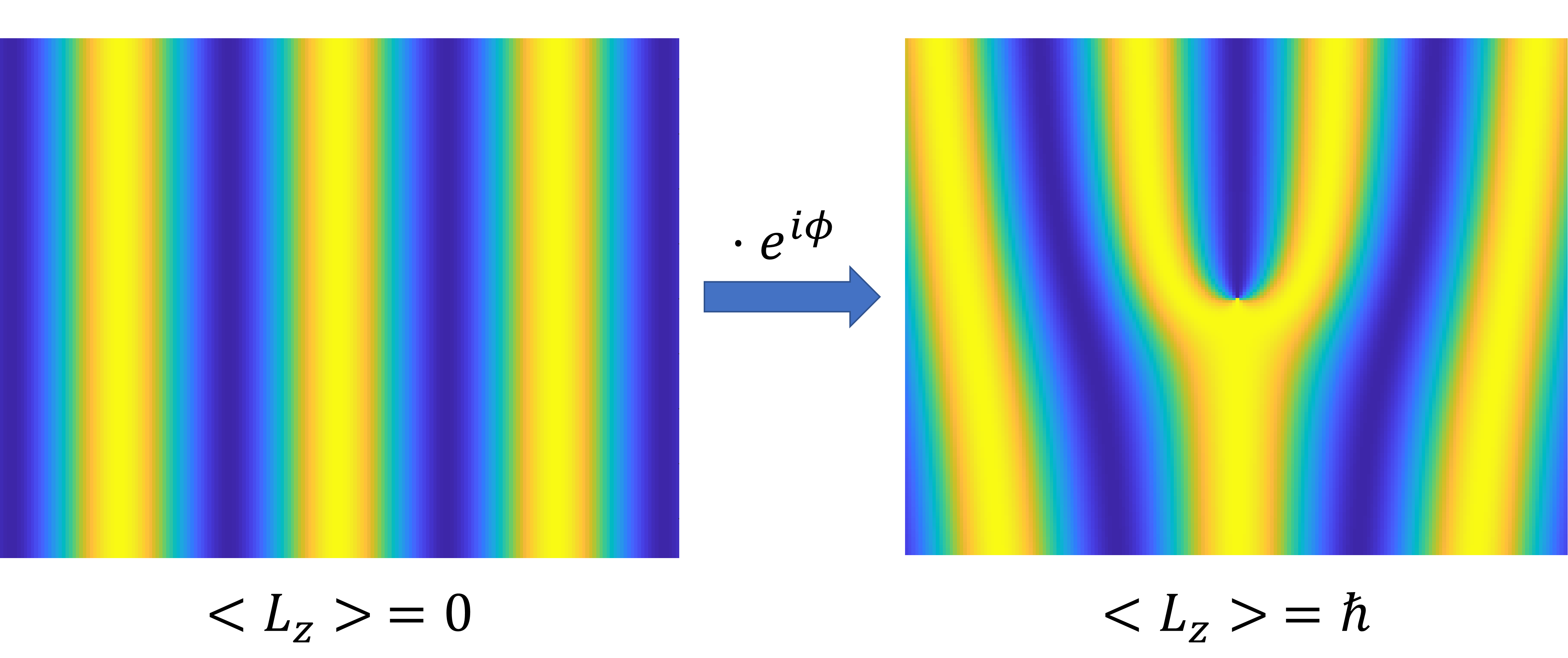
Below a figure can be seen depicting a planewave with no transverse orbital angular momentum. This planewave is multiplied by the transverse orbital angular momentum raising operator, thereby increasing the orbital angular momentum by one unit of . The wavefronts appear to show a forked pattern, with a phase singularity at the center. While this does not accurately represent the action of an electric field on a planewave, the figure does give an idea as to how transverse orbital angular momentum presents itself.