Tight State-Independent Preparation Uncertainty Relations for Qubits

In our latest neutron polarimetric experiment ¹ we study tight state-independent preparation uncertainty relations for quits, as proposed by Abbott et al  in ². (see here for theoretical details). The recent interest in measurement uncertainty relations revealed that the well-known Robertson-Schrödinger uncertainty relation lacks an irreducible or state-independent lower bound. Consequently, Abbott et al. proposed state-independent uncertainty relations for arbitrary Pauli observables and of a two-level system (qubit), expressed as in terms of expectation values. It is a peculiarity of the qubit system, that there is a one-to-one correspondence between the expectation value and the standard deviation, that is a measure of uncertainty. The same argument also applies to Shannon entropies. Hence, the relations are expressed in two measures of uncertainty,  standard deviation and entropy, which are both functions of the expectation value, as illustrated in the experimental scheme below (see here for details of the experiment and more results).

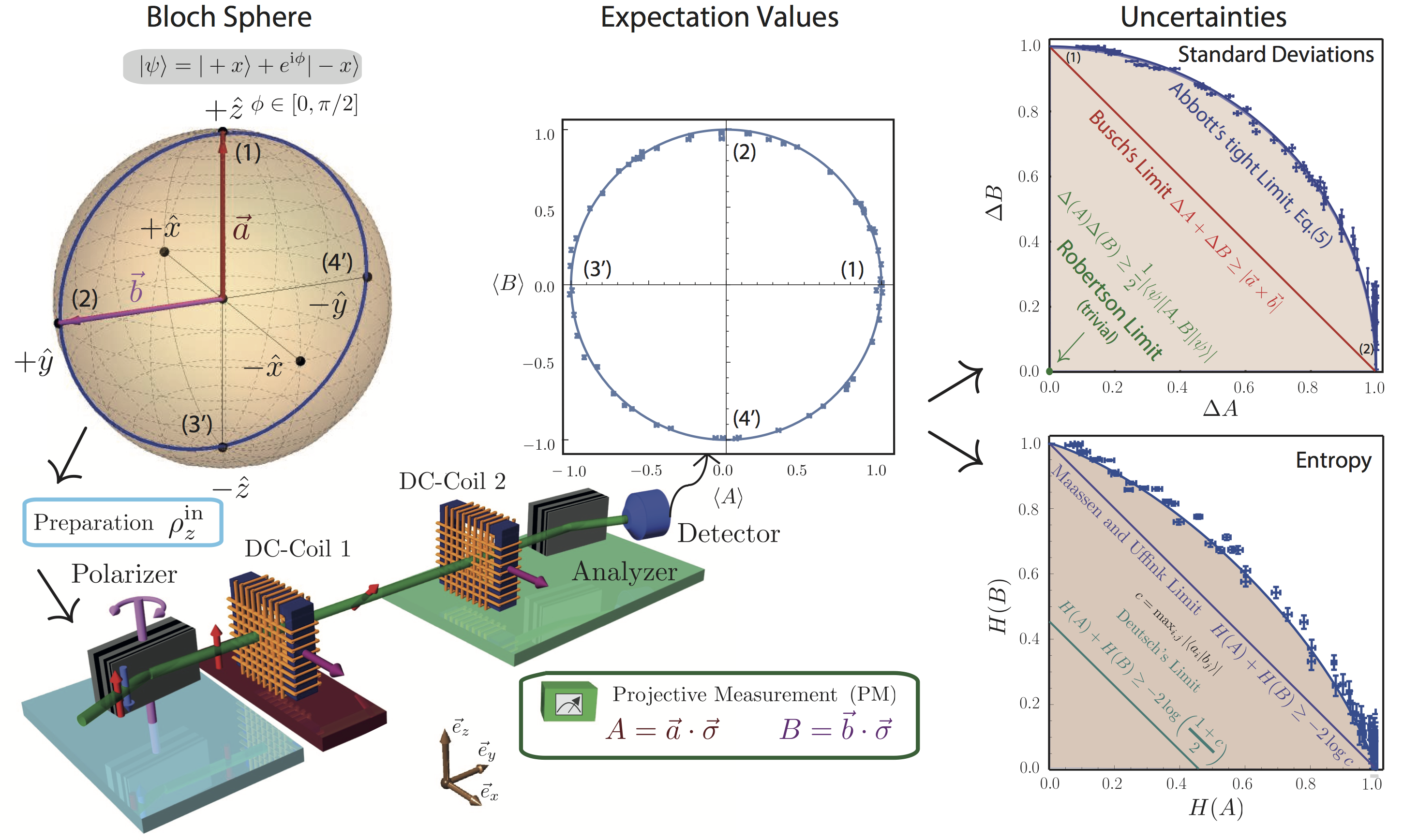
The tight relations in terms of standard deviations are compared to the trivial Robertson limit (which is zero for the given initial states) and to limits from Busch, which are only saturated in two points. The uncertainty relations in terms of entropies are compared to the suboptimal bound of Deutsch and to the well-known Maasen Uffink relations, which are saturated only in two points.

The tightness of state-independent  uncertainty relations for Pauli measurements on qubits is experimentally demonstrated. In addition, we observed bounds on these relations, expressed in terms of the norm of the Bloch vector, resulting in (partially) state-dependent uncertainty relations with lower bounds. We have experimentally confirmed the tightness of state-independent, as well as partially state-dependent, uncertainty relations for pairs of Pauli measurements on qubits. The observed uncertainty relations, expressed in terms of standard deviations and Shannon entropy (both functions of the expectation value), completely characterize the allowed values of uncertainties for Pauli spin observables. 

1.  S. Sponar, A. Danner, K. Obigane, S. Hack, and Y. Hasegawa, Phys. Rev. A 102, 042204 (2020). ↩

2. A. A. Abbott P-L Alzieu, M. J. W. Hall and C. Branciard, Mathematics 4, 8 (2016). ↩