Test of completeness of quantum root-mean-square errors

In our latest work ¹ we study the reliability of errors in the quantum measuring process via neutron spin measurements. According to the uncertainty principle, which is a corner stone of quantum mechanics, it is impossible to measure both position and momentum of an elementary particle (e.g. electron as in Heisenberg’s original argument) with arbitrary accuracy or in other word with  zero error. Therefore, it is necessary to accurately grasp the error of a auntum measurment with an appropriate definition, which has been an nontrivial task for several decades.  One of the major problems in quantum physics has been to generalize the classical root-mean-square error to quantum measurements to obtain an error measure satisfying both soundness (to vanish for any accurate measurements) and completeness (to vanish only for accurate measurements). A noise-operator-based error measure has been commonly used for this purpose, but it has turned out incomplete. Recently, Ozawa proposed an improved definition for a noise-operator-based error measure to be both sound and complete. Recently, Ozawa proposed an improved definition for a noise-operator-based error measure to be both sound and complete. Here, we present a neutron optical demonstration for the completeness of the improved error measure for both projective (or sharp) as well as generalized (or unsharp) measurements. We present a neutron-optical test of completeness of the operator-based rms-error in quantum measurements.

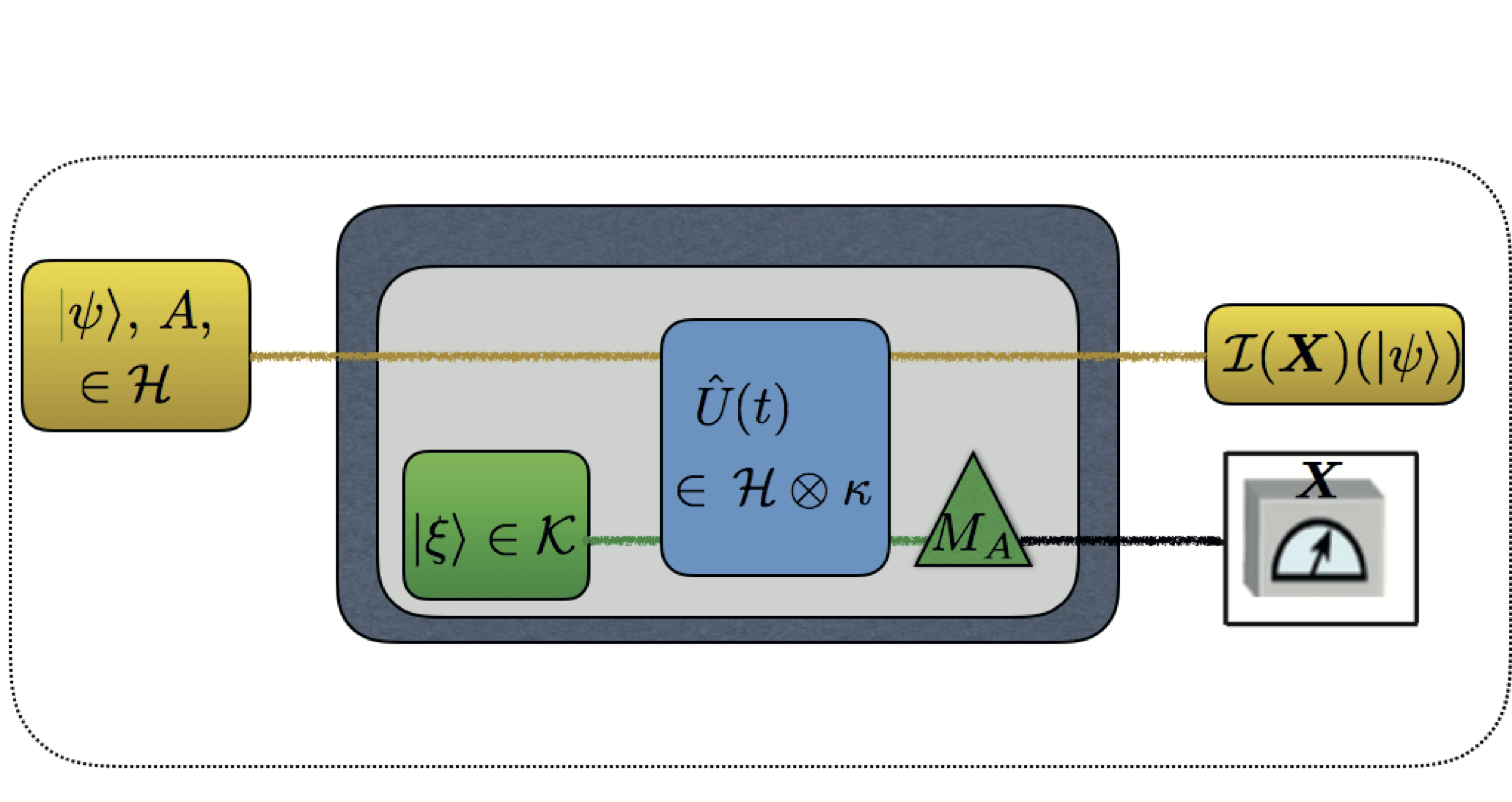
The error is usually defined as “the difference between the true value (the value that should be obtained by the ideal measurement) and the measured value (the value obtained by the actual measurement)”. In the framework of modern quantum measurement theory, the “true value” can be expressed as a physical quantity to be measured, and the “measured value” can be expressed as a physical quantity representing the value of the meter immediately after measurement. However, in quantum physics, physical quantities are represented by matrices (operators). Therefore, the physical quantity that represents the difference between the “true value” and the “measured value” is called the “error operator”, and its root mean square is called the “quantum root mean square error”, which is schematically illustrated below on the left side (see here for details of the experiment and more results).

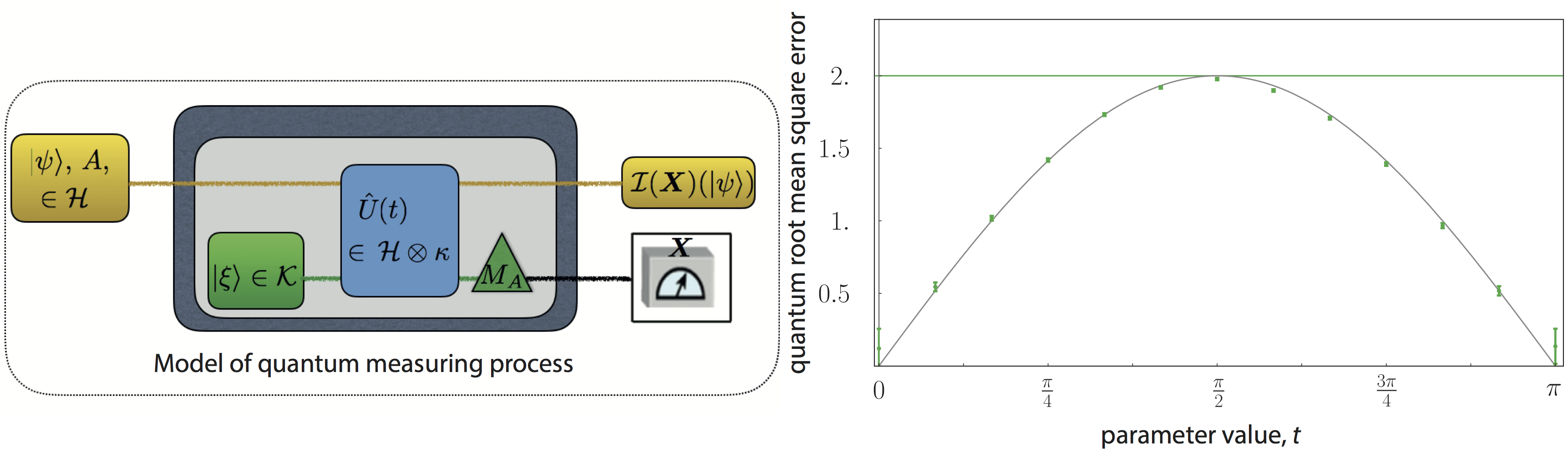
In our experiment, the “quantum root mean square (rms) error” of a neutron spin measurement is evaluated, using the state-of-the-art neutron polarimeter instrument NepTUn  located at the tangential beam portof the 250 kW TRIGA reactor at the Atominstitut – TU Wien. The rms error is evaluated by changing the initial state input to the measuring instrument by the default parameter value. After finding the “root mean square error” for each parameter value, the “local uniform root mean square error” can be obtained by continuously changing the parameter values and finding the maximum value. In this experiment, the value of “quantum root mean square error” with respect to the initial state is 0, but it is known that this measurement is not an accurate measurement. If the initial state is changed by the parameter value t, the value of “quantum root mean square error” changes to 2 | sin t | in theory. The experimental data reproduced the theoretical values with high accuracy for 13 values with 0 < t < π. Therefore, by continuously changing the parameter value, the maximum value of “local uniform quantum squared mean square error” of 2 can be obtained. In other words, the error hidden in the error value 0 according to the conventional definition in the original initial state appears as the error value 2 | sin t | when the initial state is changed by the parameter value t. Therefore, the prediction of Ozawa’s theory that the maximum value 2 is obtained as the original error value was verified by experiments, as can be seen above in the right plot.

1. S. Sponar, A. Danner, M. Ozawa, and Y. Hasegawa, npj Quantum Information 7, 106 (2021). ↩