News
March 6, 2019
Published by Stephan Sponar
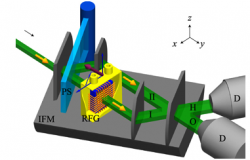
A rotating field generator is designed for an interferometer experiment. Its magnetic field is simulated, an according coil mount as well as a water cooler are fabricated and the device is successfully tested in a polarimeter experiment. The field simulations show a sufficient field homogeneity. Although the field transition is initially indicated as too long, the experimental results accord qualitatively with the assumption of a sudden field transition. The presented rotating field generator is suited for the proposed experiment by Mashhoon et al. investigating spin-rotation coupling in neutron interferometry.
Armin Danner, Bülent Demirel, Stephan Sponar and Yuji Hasegawa, J. Phys. Commun. 3, 035001 (2019). (6 March 2019)
January 31, 2019
Published by Stephan Sponar
In our latest neutron optical experiment we test the joint-measurement noise trade-off for variouse Pauli observables by implementing four-outcome positive-operator valued measure POVMs. The noise associated to the measurement of an observable is defined via conditional Shannon entropies and a tradeoff relation between the noises for two arbitrary spin observables is demonstrated. The optimal bound of this tradeoff is experimentally obtained for various non-commuting spin observables. For some of these observables this lower bound can be reached with projective measurements, but we observe that, in other cases, the tradeoff is only saturated by general quantum measurements (i.e., positive-operator valued measures), as predicted theoretically. Bülent Demirel, Stephan Sponar, Alastair A. Abbott, Cyril Branciard, and Yuji Hasegawa, New J. Phys 21,013038 (2019) (31 January 2019)
May 10, 2018
Published by Stephan Sponar
In our latest neutron optical experiment we investigate the paths taken by neutrons in a three – beam interferometer. In various beam-paths of the interferometer, the energy of the neutrons is partially shifted so that the faint traces are left along the beam-path. Which-path information is extracted from these faint traces with minimal-perturbations. Theory is derived by simply following the time evolution of the wave function of the neutrons, which clarifies the observation in the framework of standard quantum mechanics. Which-way information is derived from the intensity, sinusoidally oscillating in time at different frequencies, which is considered to result from the interfering cross terms between stationary main component and the energy-shifted which-way signals. Final results give experimental evidence that the partial wave functions of the neutrons in each beam path are superimposed and present in multiple locations in the interferometer. Hermann Geppert-Kleinrath, Tobias Denkmayr, Stephan Sponar, Hartmut Lemmel, Tobias Jenke, and Yuji Hasegawa, Phys. Rev. A 97, 052111 (2018) (10 May 2018)
November 29, 2017
Published by Stephan Sponar
Contextuality is one of the most counterintuitive aspects of quantum mechanics. While previous contextuality experiments have only been able to demonstrate the global incompatibility between the predictions of quantum mechanics and non-contextual hidden variable theories , but failed to isolate precisely where that incompatibility occurs. We could show, for the first time, that quantum contextuality can be confined to specific observables, which also manifests in a violation of the pigeon hole principle. M. Waegell, T. Denkmayr, H. Geppert, D. Ebner, T. Jenke, Y. Hasegawa, S. Sponar, J. Dressel, J. Tollaksen, Physical Review A 96, 052131 (2017) (27 November 2017)
September 4, 2017
Published by Stephan Sponar
Since the theoretical findings of Masanao Ozawa, namely a violating and thus a necessary reformulation of Heisenberg’s original error-disturbance uncertainty relation, this particular field has experienced increased attention. However, soon after publication of our experimental verification an alternative theory was presented by Paul Busch, and Pekka Lahti, and Reinhard F. Werner (BLW) which in contrast stated the validity of Heisenberg’s relation. We now carried out the first experimental comparison of these two competing approaches leading to a surprising result: Despite the strong controversy, in case of projectively measured qubit observables both approaches even lead to equal outcomes. S. Sponar and G. Sulyok, Physical Review A 96 022137 (2017) (28 August 2017)
January 7, 2017
Published by Stephan Sponar
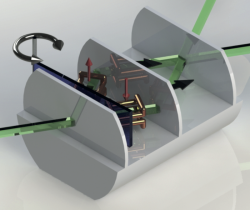
We developed a measurement scheme, used in a matter-wave interferometric experiment, in which the neutron path system’s quantum state was characterized via direct measurements using both strong and weak interactions. Experimental evidence is given that strong interactions outperform weak ones for tomographic accuracy. Our results are not limited to neutron interferometry, but can be used in a wide range of quantum systems. T. Denkmayr et al., Physical Review Letters 118, 010402 (2017) (6 January 2017)
September 30, 2016
Published by Stephan Sponar
In the last decade, several universally valid forms of error-disturbance uncertainty relations were derived for completely general quantum measurements for arbitrary states. An optimal form for spin measurements for some pure states was established recently. However, the bound in his inequality is not stringent for mixed states. Masanao Ozawa derived a new bound tight in the corresponding mixed state case, which was tested by our group. We experimentally observed the attainability of the new bound. B. Demirel et al., Physical Review Letters 117, 140402 (2016) (27 September 2016)
July 13, 2015
Published by Stephan Sponar
Uncertainty relation in quantum information theory publish in PRL and relieved an Editor’s Suggestion! Information is a key quantity in science and plays a significant role in many economic sectors such as communication technologies, cryptography, or data storage. In quantum communication and information technology the transfer and encryption of information is studied. Sulyok et al., Phys. Rev. Lett. 115, 030401 (2015) (13 July 2015)
July 29, 2014
Published by Stephan Sponar
The Cheshire Cat featured in Lewis Caroll’s novel “Alice in Wonderland” is a remarkable creature: it disappears, leaving its grin behind. Can an object be separated from its properties? Denkmayr et al., Nat. Commun. 5, 4492 (2014) (29 July 2014)
January 16, 2012
Published by Stephan Sponar
Heisenberg’s uncertainty principle. is certainly one of the most famous foundations of quantum physics. According to this principle, not all properties of a quantum particle are determined with arbitrary accuracy. In the early days of quantum theory, this has often been justified by the notion that every measurement inevitably recoils the quantum particle, which disturbs the results of any further measurements. This, however, turns out to be an oversimplification. In our neutron polarimetric experiment different sources of quantum uncertainty could now be distinguished, validating theoretical results of an error-disturbance uncertainty relation proposed by Masanao Ozawa. Y. Hasegawa et al., Nature Physics 8, 185-189 (2012) (15 January 2012)