Spekkens’ Toy Bit

We now focus our attention to the simplest case: a single toy bit, which is illustrated below on the left side. It is a system that can be in one of four states, labelled (−, −), (−, +), (+, −) and (+, +) in the -plane. The ontic state is represented by the values (x, y), with ± short for ±1. The most precise description our toy bit is always its ontic state, but we might not know exactly. Our knowledge of the system is described by a probability distribution over the four ontic states, and this probability distribution is our epistemic state. But there is a restriction on the set of epistemic states that may be assigned to the system, called the knowledge-balance principle (a kind of uncertainty principle), stating at most half of the information needed to specify the ontic state can be known at any given time, the first requirement on our model. So for example, that if we know the -coordinate with certainty then we cannot know anything about the -coordinate. Given this restriction, there are six possible states of maximal knowledge, termed pure states, as shown below in the middle. They are denoted as and  in analogy to the quantum states and  . Note that the epistemic states   are not states with a definite value of the -coordinate, since the system is two dimensional. Instead, is the state in which we know only that the and coordinates are equal and is the state in which we know only that they are different.

The next step, after preparation of the epistemic states, is to describe the measurement process in such manner that if a measurement is repeated twice in succession then it should yield the same outcome both times, i.e., the measurement has to be repeatable. In addition, the measurement should respect the knowledge balance principle, which is achieved by introducing a second requirement, namely that the measurement must necessarily cause a disturbance to the ontic state, since otherwise we could determinate  ontic state exactly (by first measuring  then ). We have three nontrivial measurements that can be implemented in such a way that they satisfy the two requirements: the measurement reveals the coordinate, the measurement the coordinate, and the measurement reveals the value of , illustrated below in the middle. Each of these measurements causes a random exchange between the pairs of ontic states that give the same outcome in the measurement: For example, if we perform an measurement and get the +1 outcome, then with probability  nothing happens and with probability  (+, −) and (+, +) are exchanged. Then the theory described so far makes exactly the same predictions as quantum theory.

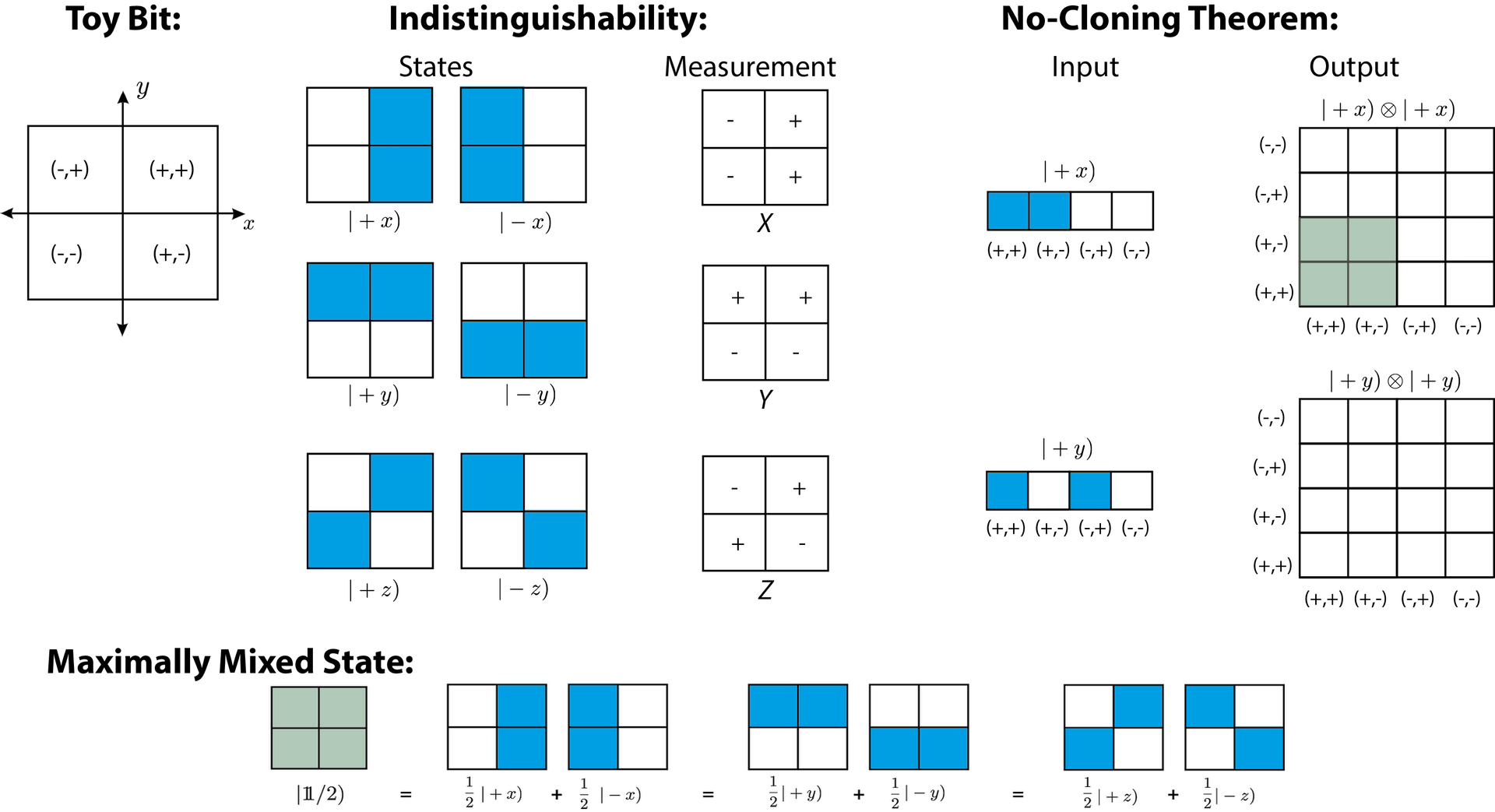
Another feature of quantum theory that is also covered by Spekkens’ model is the no-cloning theorem, stating that in quantum theory, there is no transformation that copies both of two non-orthogonal states (see here for details on the no-cloning theorem). In quantum mechanics there exists no apparatus that outputs both when is input and when is input. In order to represent a two toy bit state, the ontic state space of a single toy bit is now represented along one dimension in our schematic illustration above on the right side. For the outputs, the horizontal axis represents the first toy bit and the vertical axis represents the second toy bit. Blue represents ontic states occupied with 50% probability and light green represents those occupied with 25% probability. The inputs overlap on an ontic state that they both assign 50% probability, but the outputs only overlap on an ontic state that they both assign 25% probability. hence the cloning apparartus is impossible. Finally, consider the fact that mixed states in quantum theory have more than one decomposition into a convex sum of pure states. The maximally mixed state ,in our toy bit theory, can be written as a 50/50 mixture in three different ways. Light green indicates again a probability of 1/4. These are only a few aspects of a possible realist –epistemic theory.