Divergence of Standard Deviations

Let us first consider the well-known single-slit experiment, which is schematically illustrated below. An incoming monochromatic plane wave, representing an incoming beam of particles. The particles with momentum passe a slit of width and diffracted particles are observed  or screen (or photographic plate) placed at a distance . 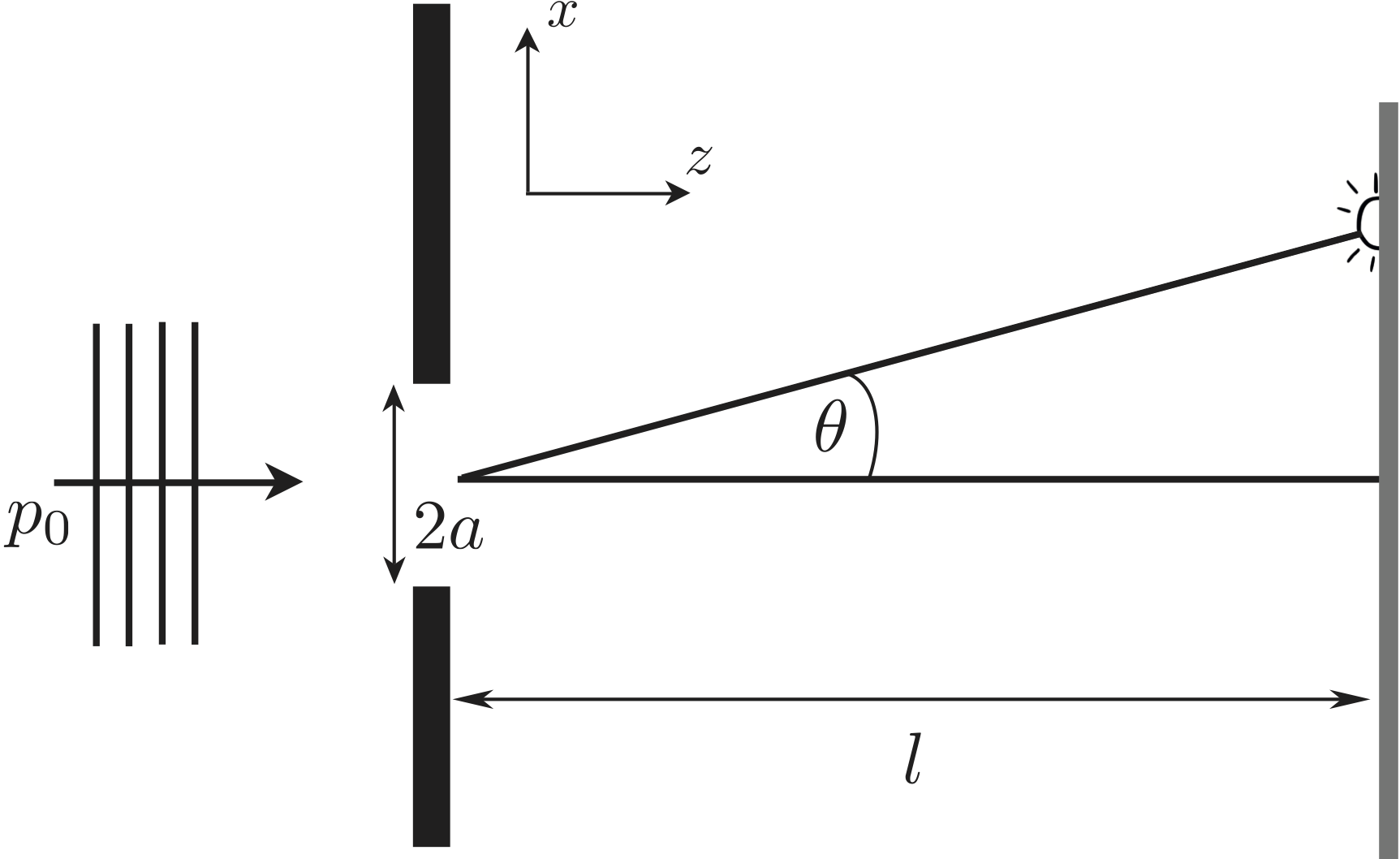Diffraction of particles by a slit is frequently used as an illustration of the uncertainty principle in the following manner: The width of the slit is taken as a measure of the uncertainty in position  at the screen, that is . The natural question then is with what precision can the momentum  directly behind the slit be predicted? The usual argument is as follows: The momentum is calculated from the angle of impact on the screen as . Hence, the momentum is unpredictable by an amount that corresponds to the width of the diffraction pattern, where as an estimate of this width one usually takes the angle subtending the first diffraction minimum, which is . From that we get  and finally  illustrating the uncertainty principle: If the width of the slit is decreased, the uncertainty in momentum increases. It is not possible to predict arbitrarily sharp values for both quantities.

Let us now try a slightly more formal description of the experiment from above ¹. The wave function at the screen () may be represented the following Fourier pair illustrated aside (for and this is a good approximation of a Fourier transform).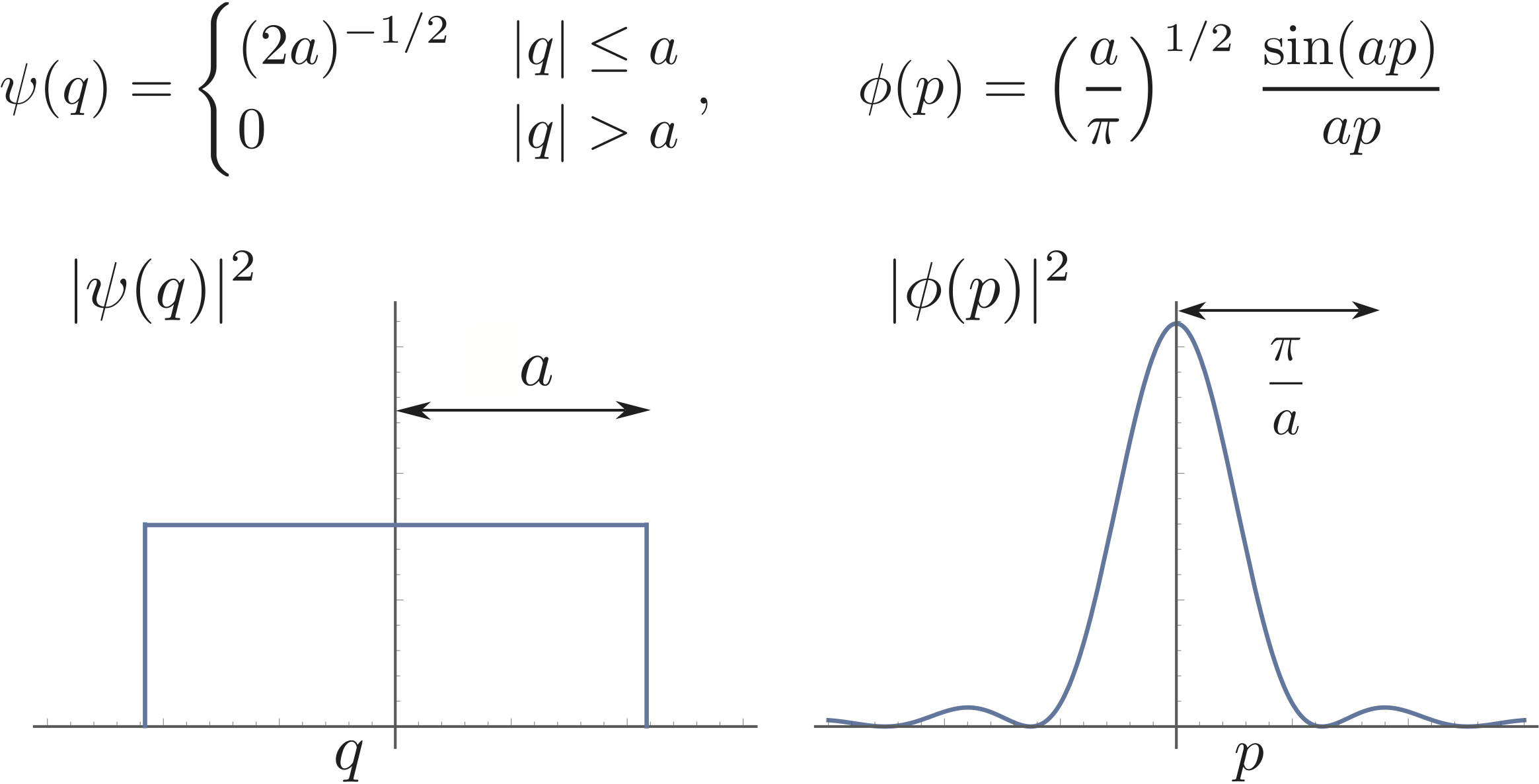 The uncertainty in momentum corresponds to the width of the central peak, which contains about 95% of the total probability. Therefore is a very reasonable measure of uncertainty. The standard deviations are then defined as and , where and , which gives and . So if we take these as measures of uncertainty, we have to say that the momentum is completely uncertain (independently ). The problem steems from the definition of where the probability density is multiplied by a factor , giving increasing weight to the distant parts of the probability distribution. Although the tails of the momentum distribution contain very little probability, they fall off too slowly for to be finite, which illustrates that the standard deviation is not a proper measure of the width of a general probability distribution (only for Gaussians).

1. J. B. M. Uffink I and J. Hilgevoord, Foundations of Physics. 15, 925 (1985).↩